BloomFilter
布隆过滤器
布隆过滤器 (Bloom Filter)是由 Burton Howard Bloom 于 1970 年提出,它是一种 space efficient 的概率型数据结构,它利用位数组很简洁地表示一个集合,用于判断一个元素是否在集合中。在垃圾邮件过滤的黑白名单方法、爬虫(Crawler)的网址判重模块中等等经常被用到。哈希表也能用于判断元素是否在集合中,但是布隆过滤器只需要哈希表的 1/8 或 1/4 的空间复杂度就能完成同样的问题。布隆过滤器可以插入元素,但不可以删除已有元素。其中的元素越多,false positive rate(误报率)越大,但是 false negative (漏报)是不可能的。

算法描述
一个 empty bloom filter 是一个有 m bits 的 bit array,每一个 bit 位都初始化为 0。并且定义有 k 个不同的 hash function,每个都以 uniform random distribution 将元素 hash 到 m 个不同位置中的一个。在下面的介绍中 n 为元素数,m 为布隆过滤器或哈希表的 slot 数,k 为布隆过滤器重 hash function 数。
为了 add 一个元素,用 k 个 hash function 将它 hash 得到 bloom filter 中 k 个 bit 位,将这 k 个 bit 位置 1。
为了 query 一个元素,即判断它是否在集合中,用 k 个 hash function 将它 hash 得到 k 个 bit 位。若这 k bits 全为 1,则此元素在集合中;若其中任一位不为 1,则此元素比不在集合中(因为如果在,则在 add 时已经把对应的 k 个 bits 位置为 1)。
不允许 remove 元素,因为那样的话会把相应的 k 个 bits 位置为 0,而其中很有可能有其他元素对应的位。因此 remove 会引入 false negative,这是绝对不被允许的。
当 k 很大时,设计 k 个独立的 hash function 是不现实并且困难的。对于一个输出范围很大的 hash function(例如 MD5 产生的 128 bits 数),如果不同 bit 位的相关性很小,则可把此输出分割为 k 份。或者可将 k 个不同的初始值(例如 0,1,2, … ,k-1)结合元素,feed 给一个 hash function 从而产生 k 个不同的数。
当 add 的元素过多时,即 n/m 过大时(n 是元素数,m 是 bloom filter 的 bits 数),会导致 false positive 过高,此时就需要重新组建 filter,但这种情况相对少见。
时间与空间优势
当可以承受一些误报时,布隆过滤器比其它表示集合的数据结构有着很大的空间优势。例如 self-balance BST, tries, hash table 或者 array, chain,它们中大多数至少都要存储元素本身,对于小整数需要少量的 bits,对于字符串则需要任意多的 bits(tries 是个例外,因为对于有相同 prefixes 的元素可以共享存储空间);而 chain 结构还需要为存储指针付出额外的代价。对于一个有 1%误报率和一个最优 k 值的布隆过滤器来说,无论元素的类型及大小,每个元素只需要 9.6 bits 来存储。这个优点一部分继承自 array 的紧凑性,一部分来源于它的概率性。如果你认为 1%的误报率太高,那么对每个元素每增加 4.8 bits,我们就可将误报率降低为原来的 1/10。add 和 query 的时间复杂度都为 O(k),与集合中元素的多少无关,这是其他数据结构都不能完成的。
如果可能元素范围不是很大,并且大多数都在集合中,则使用确定性的 bit array 远远胜过使用布隆过滤器。因为 bit array 对于每个可能的元素空间上只需要 1 bit,add 和 query 的时间复杂度只有 O(1)。注意到这样一个哈希表(bit array)只有在忽略 collision 并且只存储元素是否在其中的二进制信息时,才会获得空间和时间上的优势,而在此情况下,它就有效地称为了 k=1 的布隆过滤器。
而当考虑到 collision 时,对于有 m 个 slot 的 bit array 或者其他哈希表(即 k=1 的布隆过滤器),如果想要保证 1%的误判率,则这个 bit array 只能存储 m/100 个元素,因而有大量的空间被浪费,同时也会使得空间复杂度急剧上升,这显然不是 space efficient 的。解决的方法很简单,使用 k>1 的布隆过滤器,即 k 个 hash function 将每个元素改为对应于 k 个 bits,因为误判度会降低很多,并且如果参数 k 和 m 选取得好,一半的 m 可被置为为 1,这充分说明了布隆过滤器的 space efficient 性。
以垃圾邮件过滤中黑白名单为例:现有 1 亿个 email 的黑名单,每个都拥有 8 bytes 的指纹信息,则可能的元素范围为
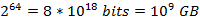
![clip_image002[]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162318585390.png)
若采用哈希表,由于大多数采用 open addressing 来解决 collision,而此时的 search 时间复杂度为:
即若哈希表半满(n/m = 1/2),则每次 search 需要 probe 2 次,因此在保证效率的情况下哈希表的存储效率最好不超过 50%。此时每个元素占 8 bytes,总空间为:
若采用 Perfect hashing(这里可以采用 Perfect hashing 是因为主要操作是 search/query,而并不是 add 和 remove),虽然保证 worst-case 也只有一次 probe,但是空间利用率更低,一般情况下为 50%,worst-case 时有不到一半的概率为 25%。
若采用布隆过滤器,取 k=8。因为 n 为 1 亿,所以总共需要
![clip_image002[1]](http://images.cnblogs.com/cnblogs_com/allensun/201102/20110216231900208.png)
所需空间比上述哈希结构小得多,并且误判率在万分之一以下。
误判概率的证明与计算
假设布隆过滤器中的 hash function 满足 simple uniform hashing 假设:每个元素都等概率地 hash 到 m 个 slot 中的任何一个,与其它元素被 hash 到哪个 slot 无关。若 m 为 bit 数,则对某一特定 bit 位在一个元素由某特定 hash function 插入时没有被置位为 1 的概率为:
则 k 个 hash function 中没有一个对其置位的概率为:
如果插入了 n 个元素,但都未将其置位的概率为:
则此位被置位的概率为:
现在考虑 query 阶段,若对应某个待 query 元素的 k bits 全部置位为 1,则可判定其在集合中。因此将某元素误判的概率为:
从上式中可以看出,当 m 增大或 n 减小时,都会使得误判率减小,这也符合直觉。
现在计算对于给定的 m 和 n,k 为何值时可以使得误判率最低。设误判率为 k 的函数为:
下面求最值
可以看出若要使得误判率 ≤1/2,则:
这说明了若想保持某固定误判率不变,布隆过滤器的 bit 数 m 与被 add 的元素数 n 应该是线性同步增加的。
布隆过滤器的设计
应用时首先要先由用户决定要 add 的元素数 n 和希望的误差率 P。这也是一个设计完整的布隆过滤器需要用户输入的仅有的两个参数,之后的所有参数将由系统计算,并由此建立布隆过滤器。
系统首先要计算需要的内存大小 m bits:
再由 m,n 得到 hash function 的个数:
至此系统所需的参数已经备齐,接下来 add n 个元素至布隆过滤器中,再进行 query。
根据公式,当 k 最优时:
因此可验证当 P=1%时,存储每个元素需要 9.6 bits:
而每当想将误判率降低为原来的 1/10,则存储每个元素需要增加 4.8 bits:
这里需要特别注意的是,9.6 bits/element 不仅包含了被置为 1 的 k 位,还把包含了没有被置为 1 的一些位数。此时的
才是每个元素对应的为 1 的 bit 位数。
此概率为某 bit 位在插入 n 个元素后未被置位的概率。因此,想保持错误率低,布隆过滤器的空间使用率需为 50%。

![clip_image002[]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162318595880.png)
![clip_image002[1]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162318599402.png)
![clip_image002[1]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319003174.png)
![clip_image002[1]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319014536.png)
![clip_image002[1]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319024470.png)
![clip_image002[2]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319021057.png)
![clip_image002[2]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319026007.png)
![clip_image002[2]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319039321.png)
![clip_image002[2]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319043367.png)
![clip_image002[2]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319045809.png)
![clip_image002[3]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319058775.png)
![clip_image002[3]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319062089.png)
![clip_image002[3]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319061466.png)
![clip_image002[3]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319075.png)
![clip_image002[3]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319071367.png)
![clip_image002[4]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319087921.png)
![clip_image002[4]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319093395.png)
![clip_image002[4]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319091169.png)
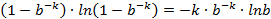
![clip_image002[4]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319101070.png)
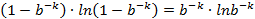
![clip_image002[4]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319117591.png)
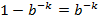
![clip_image002[4]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319127492.png)
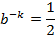
![clip_image002[4]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319136280.png)

![clip_image002[4]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319143673.png)
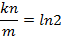
![clip_image002[4]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319159637.png)
![clip_image002[5]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319164554.png)
![clip_image002[5]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319171980.png)
![clip_image002[5]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319184946.png)
![clip_image002[5]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319181848.png)
![clip_image002[6]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319199274.png)
![clip_image002[5]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319207779.png)
![clip_image002[6]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319219076.png)
![clip_image004[]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319227515.png)
![clip_image002[7]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319233238.png)
![clip_image002[7]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319248156.png)
![clip_image002[7]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319257533.png)
![clip_image002[7]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319256072.png)
![clip_image002[7]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319266562.png)
![clip_image002[8]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319269877.png)
![clip_image002[8]](http://images.cnblogs.com/cnblogs_com/allensun/201102/201102162319272003.png)