归并排序

合并排序也是典型的分而治之的思想，其将复杂的问题分割为多个子问题，对子问题分别求解然后合并为最终的结果。合并排序主要包含两个步骤：分割与合并，将两个长为 N/2 的有序数组，在 N 个操作内合并为某个长为 N 的有序数组。在分割过程中，数组会被逐步切分为多个单元数组，而在合并过程中，会从单元数组开始逐步向上合并。

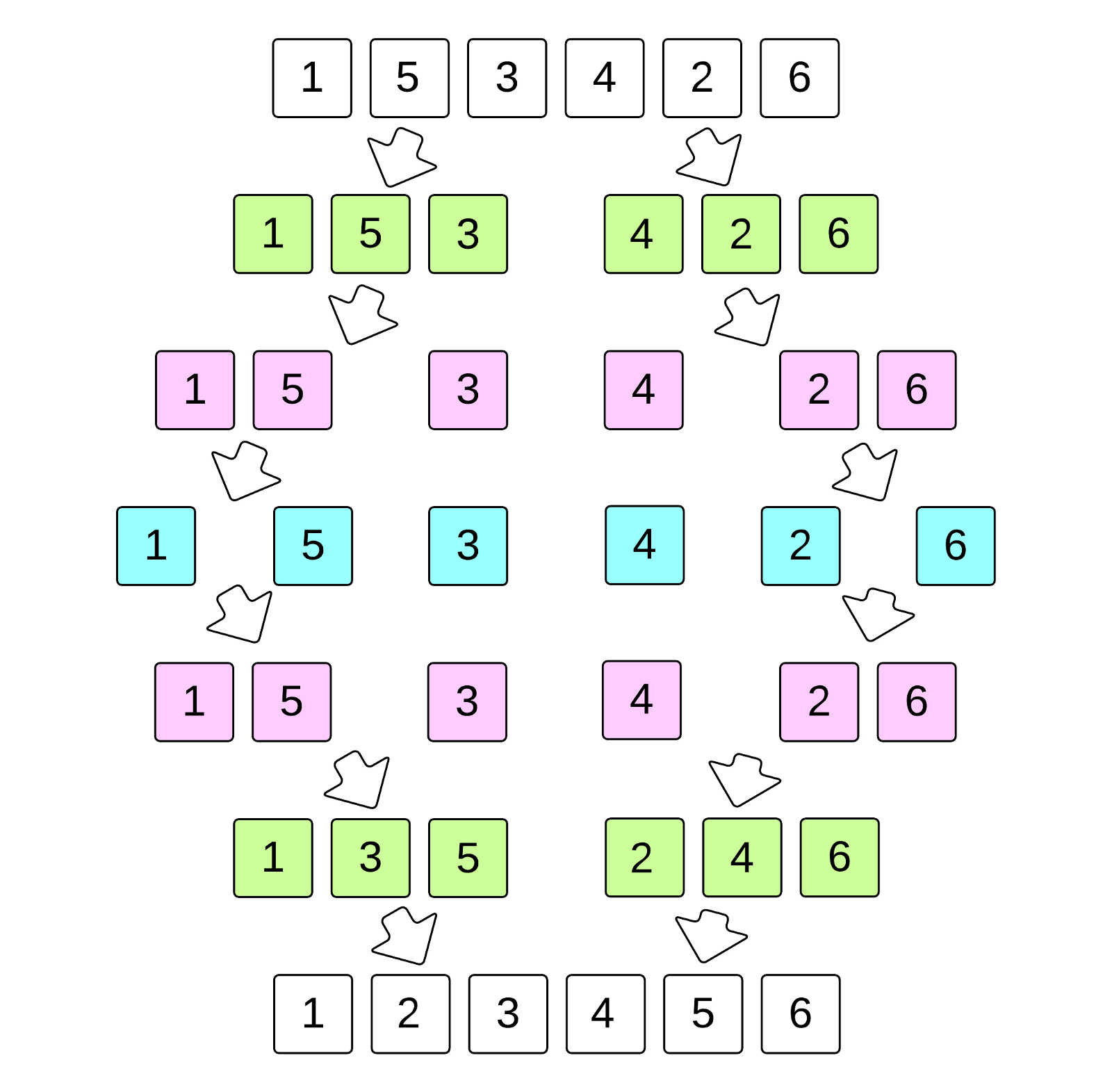
算法思想

归并排序的步骤如下：

• 判断参数的有效性，也就是递归的出口；
• 首先什么都不管，直接把数组平分成两个子数组；
• 递归调用划分数组函数，最后划分到数组中只有一个元素，这也意味着数组是有序的了；
• 然后调用排序函数，把两个有序的数组合并成一个有序的数组；
• 排序函数的步骤，让两个数组的元素进行比较，把大的/小的元素存放到临时数组中，如果有一个数组的元素被取光了，那就直接把另一数组的元素放到临时数组中，然后把临时数组中的元素都复制到实际的数组中；

归并排序的伪代码如下：

array mergeSort(array a)
   if(length(a)==1)
      return a[0];
   end if

   // recursive calls
   [left_array right_array] := split_into_2_equally_sized_arrays(a);
   array new_left_array := mergeSort(left_array);
   array new_right_array := mergeSort(right_array);

   // merging the 2 small ordered arrays into a big one
   array result := merge(new_left_array,new_right_array);
   return result;

复杂度与稳定性

归并排序的时间复杂度主要体现在两个方面，分别是数组划分函数 mergeSort 与有序数组归并函数 merge。其中 merge 函数的时间复杂度为 O(n)，因为代码中有 2 个长度为 n 的循环(非嵌套)，所以时间复杂度则为 O(n)。归并的空间复杂度就是那个临时的数组和递归时压入栈的数据占用的空间：n + logn，所以空间复杂度为 O(n)。

归并排序被广泛使用在数据库引擎中，因为其包含以下特性：

• 合并排序也是所谓的 In-place 算法，我们可以通过直接修改输入序列而不不是创建新的序列来节省内存空间
• 合并排序并不需要将所有的数据都加载到内存中，可以只向内存中加载当前处理的部分，在仅仅 100MB 的内存缓冲区内排序一个几个 GB 的表；从而同时使用磁盘空间和少量内存而避免巨量磁盘 IO。
• 合并排序支持并发操作，能够在多处理器、多线程以及多服务器上运行。

代码实现