三维几何变换

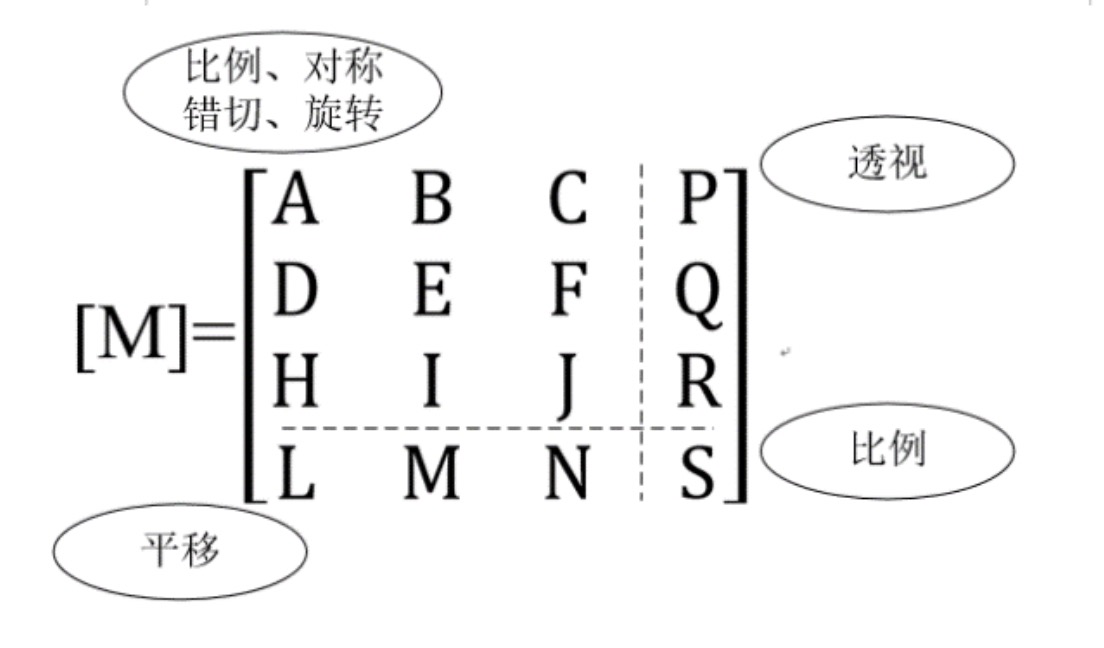
三维图形的基本变换有：三维比例变换、三维对称变换、三维错切变换、三维旋转变换。和二维图形一样，用适当的变换矩阵也可以对三维图形进行各种几何变换。对三维空间的点如（x，y，z），可用齐次坐标表示为（x，y，z，1）或（x，y，z，h），三维空间里的点的变换可写为：

$$ \left[\begin{array}{lll} x^{\prime} & y^{\prime} & z & 1 \end{array}\right]=\left[\begin{array}{lll} x & y & z & 1 \end{array}\right][M] $$

其中[M]是 4*4 阶变换矩阵，即：