05-线性代数
05-线性代数
本节目录
1. 线性代数基础知识
这部分主要是由标量过渡到向量,再从向量拓展到矩阵操作,重点在于理解矩阵层面上的操作(都是大学线代课的内容,熟悉的可以自动忽略)
1.1 标量

1.2 向量
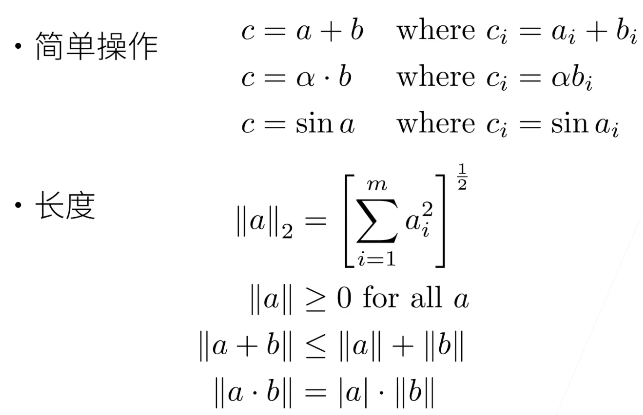
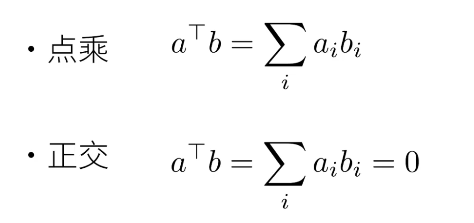
1.3 矩阵
1.3.1 矩阵的操作

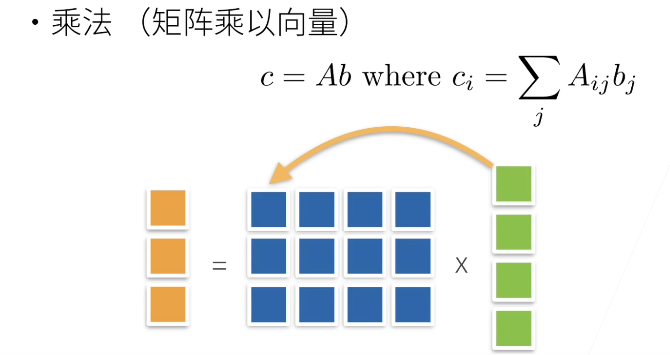
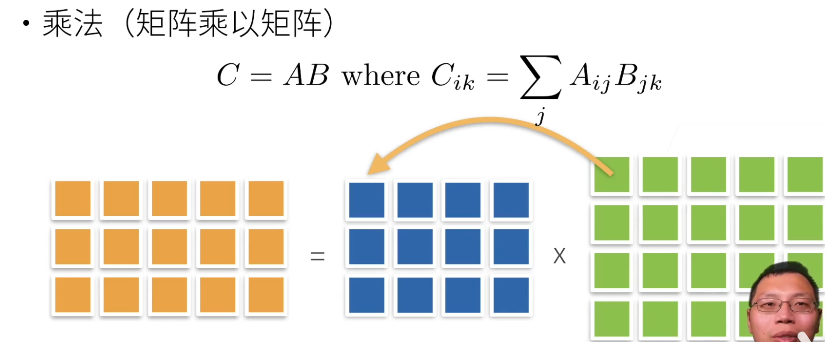

(矩阵范数麻烦且不常用,一般用 F 范数)
1.3.2 特殊矩阵
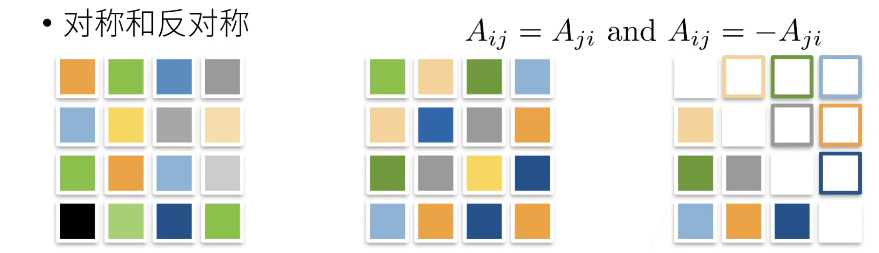
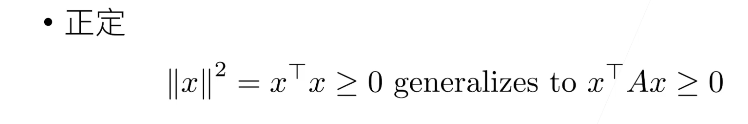

(深度学习里基本不会涉及到正定、置换矩阵,这里明确个概念就行)
1.3.3 特征向量和特征值
-
数学定义:设 A 是 n 阶方阵,如果存在常数
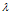

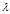
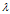
-
直观理解:不被矩阵 A 改变方向的向量 x 就是 A 的一个特征向量
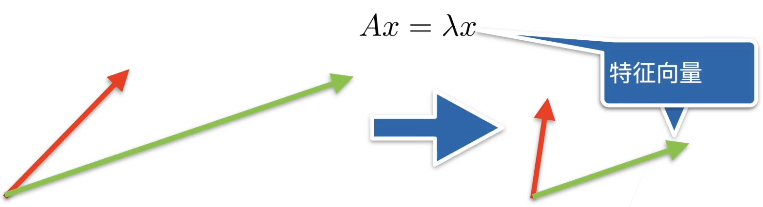
-
矩阵不一定有特征向量,但是对称矩阵总是可以找到特征向量
2. 线性代数实现
这部分主要是应用 pytorch 实现基本矩阵操作,同样由标量过渡到向量最后拓展到矩阵
2.1 标量
import torch # 应用pytorch框架
# 标量由只有一个元素的张量表示
x = torch.tensor([3.0]) # 单独一个数字表示标量也可以
y = torch.tensor([2.0]) # 单独一个数字表示标量也可以
print(x + y) # tensor([5.])
print(x * y) # tensor([6.])
print(x / y) # tensor([1.5000])
print(x ** y) # tensor([9.]) 指数运算
2.2 向量
# 向量可以看作是若干标量值组成的列表
x = torch.arange(4) # tensor([0, 1, 2, 3])
# 生成[0, 4)范围内所有整数构成的张量tensor
print(x[3]) # tensor(3)
# 和列表相似,通过张量的索引访问元素
print(len(x)) # 4
# 获取张量x的长度
print(x.shape) # torch.Size([4])
# 获取张量形状,这里x是只有一个轴的张量因此形状只有一个元素
2.3 矩阵
2.3.1 创建
A = torch.arange(6) # tensor([0, 1, 2, 3, 4, 5])
B = torch.tensor([[1,2,3],[2,0,4],[3,4,5]])
C = torch.tensor([[[1,2,3],
[4,5,6],
[7,8,9]],
[[0,0,0],
[1,1,1],
[2,2,2]]])
D = torch.arange(20, dtype=torch.float32)
2.3.2 转置
A = torch.arange(6) # tensor([0, 1, 2, 3, 4, 5])
A = A.reshape(3,2) # tensor([[0, 1],
# [2, 3],
# [4, 5]])
A = A.T # 转置 A.T
# tensor([[0, 2, 4],
# [1, 3, 5]])
2.3.3 reshape
# 使用reshape方法创建一个形状为3 x 2的矩阵A
A = torch.arange(6) # tensor([0, 1, 2, 3, 4, 5])
A = A.reshape(3,2) # tensor([[0, 1],
# [2, 3],
# [4, 5]])
tips(确定矩阵 shape):
由外层到内层依次去中括号,并记下去掉中括号后此时元素的个数,任选其中一个元素重复上述去括号的操作直到该元素中无中括号,记下的数字从左到右依次排序中间用 x 连接即为矩阵 shape
2.3.4 clone
A = torch.arange(20, dtype=torch.float32)
A = A.reshape(5,4)
B = A.clone() # 通过分配新内存,将A的一个副本分给B,该边B并不影响A的值
print(B) # tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.],
# [12., 13., 14., 15.],
# [16., 17., 18., 19.]])
2.3.5 sum
A = torch.tensor([[[1,2,3],
[4,5,6],
[7,8,9]],
[[0,0,0],
[1,1,1],
[2,2,2]]])
print(A.shape)
# torch.Size([2, 3, 3])
print(A.sum())
# tensor(54)
print(A.sum(axis=0))
"""
tensor([[ 1, 2, 3],
[ 5, 6, 7],
[ 9, 10, 11]])
"""
print(A.sum(axis=0, keepdims=True))
"""
tensor([[[ 1, 2, 3],
[ 5, 6, 7],
[ 9, 10, 11]]])
"""
print(A.sum(axis=1))
"""
tensor([[12, 15, 18],
[ 3, 3, 3]])
"""
print(A.sum(axis=1, keepdims=True))
"""
tensor([[[12, 15, 18]],
[[ 3, 3, 3]]])
"""
print(A.sum(axis=2))
"""
tensor([[ 6, 15, 24],
[ 0, 3, 6]])
"""
print(A.sum(axis=2, keepdims=True))
"""
tensor([[[ 6],
[15],
[24]],
[[ 0],
[ 3],
[ 6]]])
"""
print(A.sum(axis=[0,1]))
# tensor([15, 18, 21])
print(A.sum(axis=[0,1], keepdims=True))
# tensor([[[15, 18, 21]]])
2.3.6 numel
A = torch.tensor([[0.,0.,0.],[1.,1.,1.]])
print(A.numel()) # 6 元素个数
2.3.7 mean
A = torch.tensor([[0.,0.,0.],[1.,1.,1.]])
print(A.numel()) # 6 元素个数
print(A.sum()) # tensor(3.)
print(A.mean()) # tensor(0.5000)
# 特定轴
A = torch.tensor([[0.,0.,0.],[1.,1.,1.]])
print(A.shape[0]) # 2
print(A.sum(axis=0)) # tensor([1., 1., 1.])
print(A.mean(axis=0)) # tensor([0.5000, 0.5000, 0.5000]) 平均值
2.3.8 dot
x = torch.tensor([0.,1.,2.,3.])
y = torch.tensor([1.,1.,1.,1.])
print(torch.dot(x, y)) # tensor(6.)
2.3.9 mm、mv
A = torch.tensor([[0,1,2],
[3,4,5]])
B = torch.tensor([[2,2],
[1,1],
[0,0]])
x = torch.tensor([3,3,3])
print(torch.mv(A, x))
"""
向量积
tensor([ 9, 36])
"""
print(torch.mm(A, B))
"""
矩阵积
tensor([[ 1, 1],
[10, 10]])
"""
2.3.10 L1、L2、F 范数
x = torch.tensor([3.0, -4.0])
print(torch.abs(x).sum()) # 向量的L1范数: tensor(7.) x中的每个元素绝对值的和
print(torch.norm(x)) # 向量的L2范数: tensor(5.) x中的每个元素平方的和开根号
A = torch.ones((4, 9))
print(torch.norm(A)) # 矩阵的F范数: tensor(6.) A中的每个元素平方的和开根号
2.3.11 运算
A = torch.arange(20, dtype=torch.float32)
A = A.reshape(5,4)
B = A.clone()
print(B) # tensor([[ 0., 1., 2., 3.],
# [ 4., 5., 6., 7.],
# [ 8., 9., 10., 11.],
# [12., 13., 14., 15.],
# [16., 17., 18., 19.]])
print(A == B)
"""
tensor([[True, True, True, True],
[True, True, True, True],
[True, True, True, True],
[True, True, True, True],
[True, True, True, True]])
"""
print(A + B)
"""
tensor([[ 0., 2., 4., 6.],
[ 8., 10., 12., 14.],
[16., 18., 20., 22.],
[24., 26., 28., 30.],
[32., 34., 36., 38.]])
"""
print(A * B)
"""
tensor([[ 0., 1., 4., 9.],
[ 16., 25., 36., 49.],
[ 64., 81., 100., 121.],
[144., 169., 196., 225.],
[256., 289., 324., 361.]])
"""
2.3.12 广播
A = torch.tensor([[1.,2.,3.],
[4.,5.,6.]])
B = A.sum(axis=1, keepdims=True)
print(B)
"""
tensor([[ 6.],
[15.]])
"""
print(A / B)
"""
tensor([[0.1667, 0.3333, 0.5000],
[0.2667, 0.3333, 0.4000]])
"""
print(A + B)
"""
tensor([[ 7., 8., 9.],
[19., 20., 21.]])
"""
print(A * B)
"""
tensor([[ 6., 12., 18.],
[60., 75., 90.]])
"""
