06-矩阵计算

06-矩阵计算

本节目录

• 1. 导数的概念及几何意义
  • 1.1 标量导数
  • 1.2 亚导数
• 2. 函数与标量，向量，矩阵
  • 2.1 f 为是一个标量
    • 2.1.1 input 是一个标量
    • 2.1.2 input 是一个向量
    • 2.1.3 input 是一个矩阵
  • 2.2 f 是一个向量
    • 2.2.1 input 是一个标量
    • 2.2.2 input 是一个向量
    • 2.2.3 input 是一个矩阵
  • 2.3 F 是一个矩阵
    • 2.3.1 input 是一个标量
    • 2.3.2 input 是一个向量
    • 2.3.3 input 是一个向量
• 3. 求导的本质
• 4. 矩阵求导的布局
  • 4.1 分子布局
  • 4.2 分母布局

1. 导数的概念及几何意义

1.1 标量导数

• 导数是切线的斜率

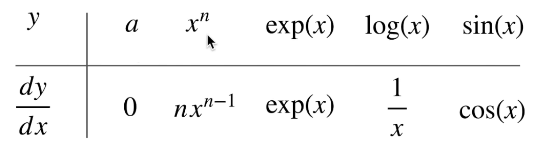
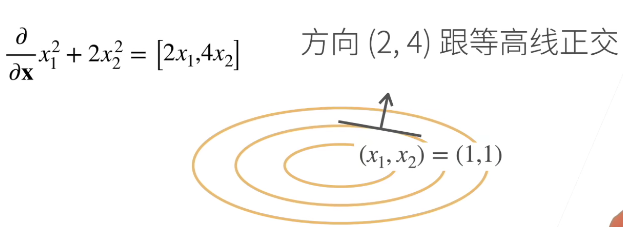
• 指向值变化最大的方向

1.2 亚导数

• 将导数拓展到不可微的函数，在不可导的点的导数可以用一个范围内的数表示

2. 函数与标量，向量，矩阵

该部分结合课程视频和参考文章进行总结（参考了知乎文章：矩阵求导的本质与分子布局、分母布局的本质（矩阵求导——本质篇） - 知乎 (zhihu.com)）

• 当 f，input 为不同形式时，f(input)结果的表达形式

2.1 f 为是一个标量

2.1.1 input 是一个标量

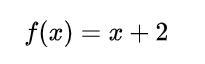
2.1.2 input 是一个向量

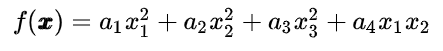
2.1.3 input 是一个矩阵

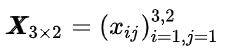
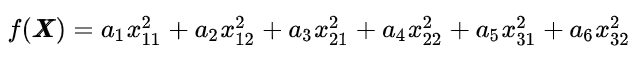
2.2 f 是一个向量

• f是由若干个 f(标量)组成的向量

2.2.1 input 是一个标量

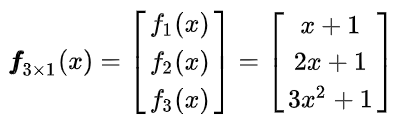
2.2.2 input 是一个向量

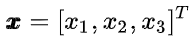
2.2.3 input 是一个矩阵

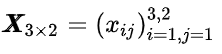
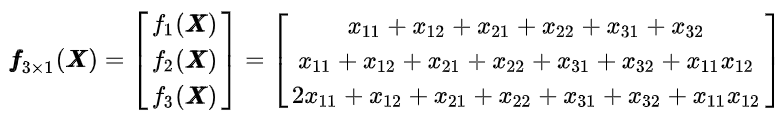
2.3 F 是一个矩阵

• F是一个由若干f组成的一个矩阵

2.3.1 input 是一个标量

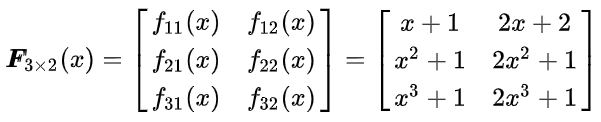
2.3.2 input 是一个向量

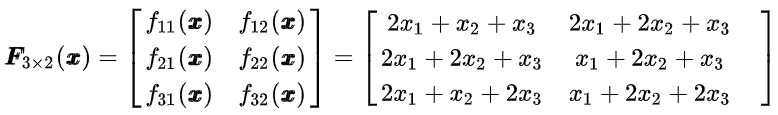
2.3.3 input 是一个向量

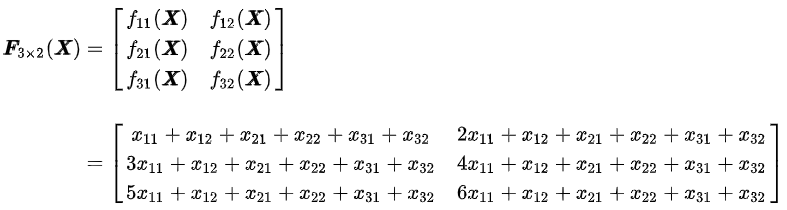
3. 求导的本质

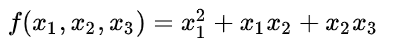
可以将 f 对 x1，x2，x3 的偏导分别求出来，即

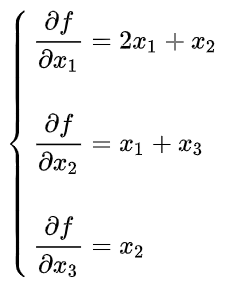
• 矩阵求导也是一样的，本质就是

  

  中的每个

  

  分别对变元中的每个元素逐个求偏导，只不过写成了向量、矩阵形式而已。

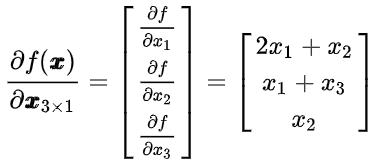
（课上是按行向量展开的）

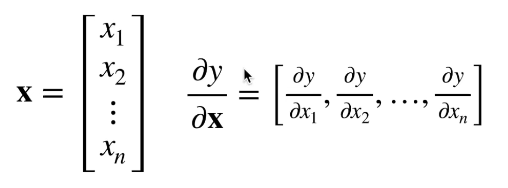
X 为矩阵时，先把矩阵变元

进行转置，再对转置后的每个位置的元素逐个求偏导，结果布局和转置布局一样。（课上讲的是这种展开方式）

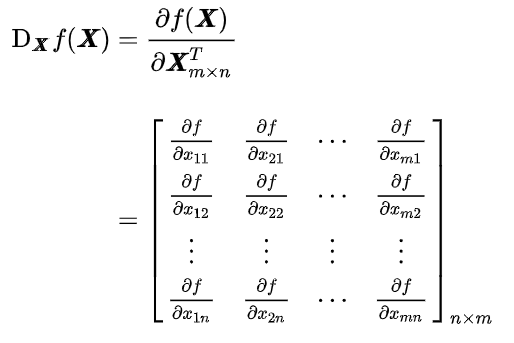
• 所以，如果

  

  中有

  

  个

  

  (标量)，变元中有

  

  个元素，那么，每个

  

  对变元中的每个元素逐个求偏导后，我们就会产生

  

  个结果。

4. 矩阵求导的布局

• 经过上述对求导本质的推导，关于矩阵求导的问题，实质上就是对求导结果的进一步排布问题 对于 2.2（f 为向量，input 也为向量）中的情况，其求导结果有两种排布方式，一种是分子布局，一种是分母布局

4.1 分子布局

分子布局，就是分子是列向量形式，分母是行向量形式 （课上讲的）

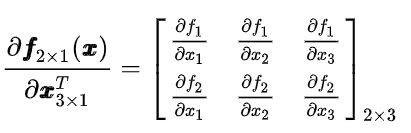
4.2 分母布局

2.分母布局，就是分母是列向量形式，分子是行向量形式

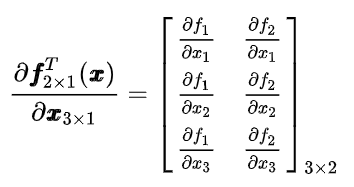
将求导推广到矩阵，由于矩阵可以看作由多个向量所组成，因此对矩阵的求导可以看作先对每个向量进行求导，然后再增加一个维度存放求导结果。

• 例如当 F 为矩阵，input 为矩阵时，F 中的每个元素 f(标量）求导后均为一个矩阵（按照课上的展开方式），因此每个f（包含多个 f（标量））求导后为存放多个矩阵的三维形状，再由于矩阵 F 由多个f组成，因此 F 求导后为存放多个f求导结果的四维形状。 对于不同 f 和 input 求导后的维度情况总结如下图所示（课程中的截图）