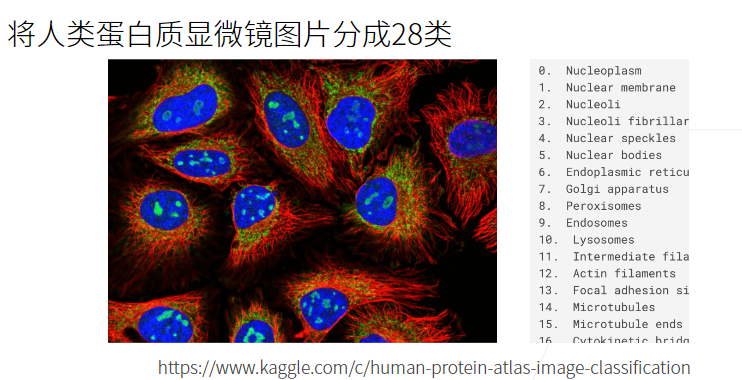
09-softmax 回归

本节目录：

• 09-softmax 回归
  • 本节目录：
  • 1.回归 VS 分类：
    • 1.1 从回归到多类分类：
      • 回归：
      • 分类：
      • 均方损失：
      • 无校验比例
      • 校验比例
    • 1.2 Softmax 和交叉熵损失
  • 2.损失函数
    • 2.1 L2 Loss
    • 2.2 L1 Loss
    • 2.3Huber’s Robust Loss
  • 3.图片分类数据集
    • 3.1 Fashion-MNIST 数据集：
  • 4.从零实现 softmax 回归
    • softmax:
  • 5.softmax 的简洁实现
  • 6.softmax 回归 Q&A

1.回归 VS 分类：

• 回归估计一个连续值
• 分类预测一个离散类别

1.1 从回归到多类分类：

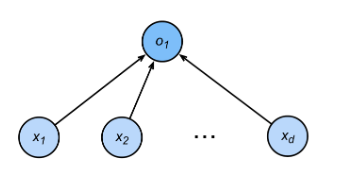
回归：

• 单连续数值输出
• 自然区间 R
• 跟真实值的区别作为损失

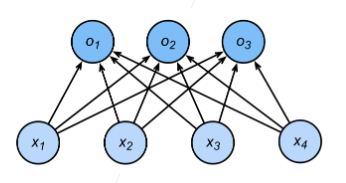
分类：

• 通常多个输出

• 输出 i 是预测为第 i 类的置信度

  

均方损失：

• 对类别进行一位有效编码

   

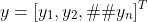
• 使用均方损失训练

• 最大值为预测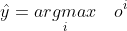 

无校验比例

• 对类别进行一位有效编码

• 最大值为预测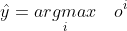 

• 需要更置信的识别正确类（大余量）  )

校验比例

• 输出匹配概率（非负，和为 1）  )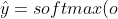

  }{\sum{k} exp(o_k)} )

• 概率 y 和$\hat{y}$的区别作为损失

1.2 Softmax 和交叉熵损失

• 交叉熵用来衡量两个概率的区别$H(p,q)=\sum_{i} -p_{i}log(q_i)$

• 将它作为损失 =-\sum*{i}y*{i}log\hat{y_{i}}=-log\hat{y_y} )

• 其梯度是真实概率和预测概率的区别 =softmax(o){i}-y{i} )

Softmax 回归是一个多类分类模型

使用 Softmax 操作子得到每个类的预测置信度

使用交叉熵来衡量和预测标号的区别

2.损失函数

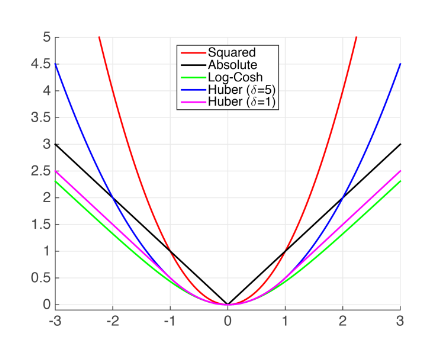
2.1 L2 Loss

=\frac{1}{2}(y-y^{’})^2 )

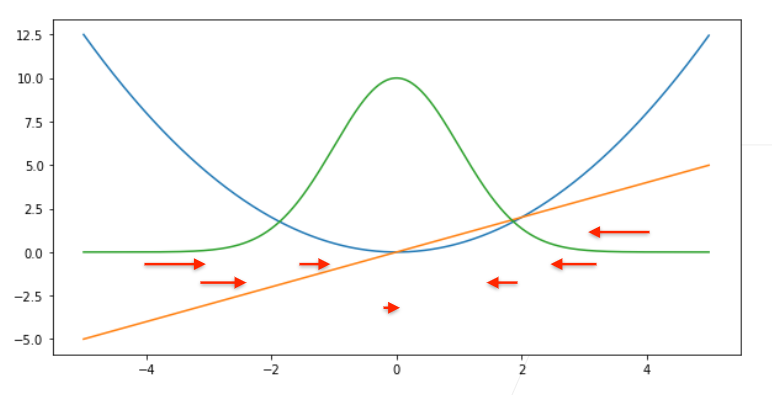
梯度会随着结果逼近而下降

2.2 L1 Loss

=\lvert y-y^{’}\rvert )

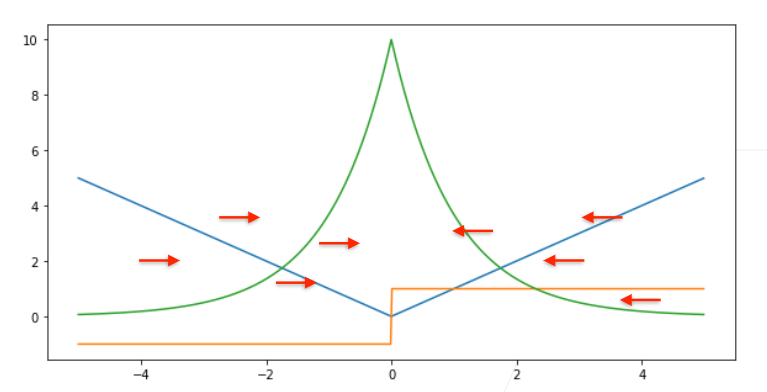
梯度保持不变，但在 0 处梯度随机

2.3Huber’s Robust Loss

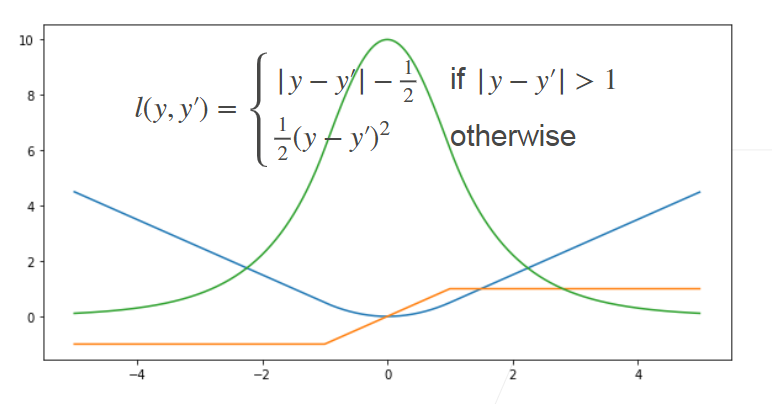
结合 L1 Loss 和 L2 Loss 的优点

3.图片分类数据集

3.1 Fashion-MNIST 数据集：

• 读取数据集

  trans=transforms.ToTensor()
  mnist_train=torchvision.datasets.FashionMNIST(root="../data",train=True,                                              transform=trans,download=True)
  mnist_test=torchvision.datasets.FashionMNIST(root="../data",train=False,                                             transform=trans,download=True)
  

• 数据集内图片大小

  mnist_train[0][0].shape
  torch.Size([1, 28, 28])
  

  表示图片为单通道（黑白）的 28X28 的图片

• 显示数据集图像

  X,y = next(iter(data.DataLoader(mnist_train,batch_size=18)))
  show_images(X.reshape(18,28,28),2,9,titles=get_fashion_mnist_labels(y))
  

  

4.从零实现 softmax 回归

softmax:

$$ softmax(X){ij}=\frac{exp(X{ij})}{\sum_{k} exp(X_{ik})} $$

def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdim=True)
    return X_exp / partition

1. 将图像展平，每个图像看做长度为 784 的向量，因为数据集有十个类别，所以网络输出维度为 10。以此设定参数大小并初始化：

   num_inputs = 784
   num_outputs = 10
   
   W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
   b = torch.zeros(num_outputs, requires_grad=True)
   

2. 实现 softmax 回归模型：

   def net(X):
       return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)
   

3. 实现交叉熵损失函数：

   def cross_entropy(y_hat, y):
       return - torch.log(y_hat[range(len(y_hat)), y])
   

4. 计算正确率：

   def accuracy(y_hat, y):
       """计算预测正确的数量"""
       if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
           y_hat = y_hat.argmax(axis=1)
       cmp = y_hat.type(y.dtype) == y
       return float(cmp.type(y.dtype).sum())
   

5. 评估 net 精度

   def evaluate_accuracy(net, data_iter):
       """计算在指定数据集上模型的精度"""
       if isinstance(net, torch.nn.Module):
           net.eval()
       metric = Accumulator(2)
       with torch.no_grad():
           for X, y in data_iter:
               metric.add(accuracy(net(X), y), y.numel())
       return metric[0] / metric[1]
   

   class Accumulator:
       """在n个变量上累加"""
       def __init__(self, n):
           self.data = [0.0] * n
   
       def add(self, *args):
           self.data = [a + float(b) for a, b in zip(self.data, args)]
   
       def reset(self):
           self.data = [0.0] * len(self.data)
   
       def __getitem__(self, idx):
           return self.data[idx]
   

6. 定义训练模型：

   def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):
       """训练模型（定义见第3章）"""
       animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                           legend=['train loss', 'train acc', 'test acc'])
       for epoch in range(num_epochs):
           train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
           test_acc = evaluate_accuracy(net, test_iter)
           animator.add(epoch + 1, train_metrics + (test_acc,))
       train_loss, train_acc = train_metrics
       assert train_loss < 0.5, train_loss
       assert train_acc <= 1 and train_acc > 0.7, train_acc
       assert test_acc <= 1 and test_acc > 0.7, test_acc
   

7. 预测：

   def predict_ch3(net, test_iter, n=6):
       """预测标签（定义见第3章）"""
       for X, y in test_iter:
           break
       trues = d2l.get_fashion_mnist_labels(y)
       preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
       titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
       d2l.show_images(
           X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])
   
   predict_ch3(net, test_iter)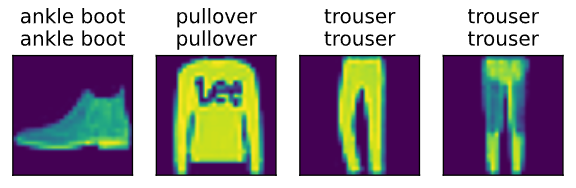
   

   

5.softmax 的简洁实现

调用 torch 内的网络层

import torch
from torch import nn
from d2l import torch as d2l
batch_size=256
train_iter,test_iter=d2l.load_data_fashion_mnist(batch_size)
net=nn.Sequential(nn.Flatten(),nn.Linear(784,10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight,std=0.01)

net.apply(init_weights)
loss=nn.CrossEntropyLoss()
trainer=torch.optim.SGD(net.parameters(),lr=0.1)
num_epochs=10
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,trainer)

6.softmax 回归 Q&A

Q1:softlabel 训练策略以及为什么有效？

softmax 用指数很难逼近 1，softlabel 将正例和负例分别标记为 0.9 和 0.1 使结果逼近变得可能，这是一个常用的小技巧。

Q2:softmax 回归和 logistic 回归？

logistic 回归为二分类问题，是 softmax 回归的特例

Q3:为什么使用交叉熵，而不用相对熵，互信息熵等其他基于信息量的度量？

实际上使用哪一种熵的效果区别不大，所以哪种简单就用哪种

Q4:

为什么我们只关心正确类，而不关心不正确的类呢？

并不是不关心，而是不正确的的类标号为零，所以算式中不体现，如果使用 softlabel 策略，就会体现出不正确的类。

Q5:似然函数曲线是怎么得出来的？有什么参考意义？

最小化损失函数也意味着最大化似然函数，似然函数表示统计概率和模型的拟合程度。

Q6:在多次迭代之后欧如果测试精度出现上升后再下降是过拟合了吗？可以提前终止吗？

很有可能是过拟合，可以继续训练来观察是否持续下降

Q7:cnn 网络主要学习到的是纹理还是轮廓还是所有内容的综合？

目前认为主要学习到的是纹理信息

Q8:softmax 可解释吗？

单纯 softmax 是可解释的，可以在统计书籍中找到相关的解释。