47-转置卷积

47-转置卷积

本节目录

• 1.转置卷积
• 2.转置卷积是一种卷积

1.转置卷积

• 转置卷积和卷积的区别：
  • 卷积不会增大输入的高宽，通常要么不变、要么减半
  • 转置卷积则可以用来增大输入高宽
• 转置卷积的具体实现：

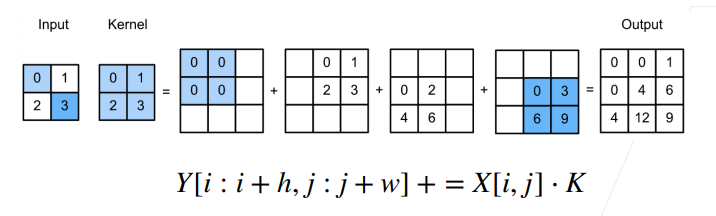
如图所示，input 里的每个元素和 kernel 相乘，最后把对应位置相加，相当于卷积的逆变换

• 为什么称之为“转置：
  • 对于卷积 Y=X*W
    • 可以对 W 构造一个 V，使得卷积等价于矩阵乘法 Y’=VX'
    • 这里 Y’,X’是 Y,X 对应的向量版本
  • 转置卷积等价于 Y’=VTX'
  • 如果卷积将输入从（h，w）变成了（h‘，w’）
    • 同样超参数的转置卷积则从（h‘，w’）变成为（h，w）

2.转置卷积是一种卷积

• 重新排列输入和核

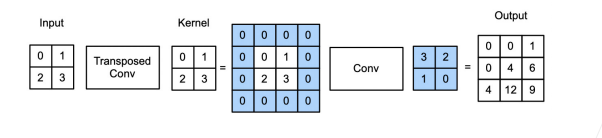
  • 当填充为 0 步幅为 1 时：
    • 将输入填充 k-1（k 时核窗口）
    • 将核矩阵上下、左右翻转
    • 然后做正常卷积（填充 0、步幅 1）
  
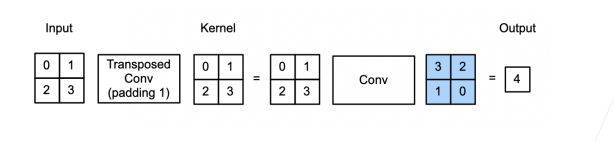
  • 当填充为 p 步幅为 1 时：
    • 将输如填充 k-p-1（k 是核窗口）
    • 将核矩阵上下、左右翻转
    • 然后做正常卷积（填充 0、步幅 1）
  

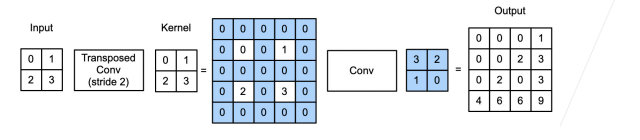
  • 当填充为 p 步幅为 s 时：

    • 在行和列之间插入 s-1 行或列

    • 将输如填充 k-p-1（k 是核窗口）

    • 将核矩阵上下、左右翻转

    • 然后做正常卷积（填充 0、步幅 1）

  

• 形状换算

  • 输入高（宽）为 n，核 k，填充 p，步幅 s：

    • 转置卷积：n‘=sn+k-2p-s

    • 卷积：n’=[(n-k-2p+s)/s]向下取整

  • 如果让高宽成倍增加，那么 k=2p+s

• 同反卷积的关系

  • 数学上的反卷积是指卷积的逆运算
    • 若 Y=conv（X,K），那么 X=deconv（Y,K）
  • 反卷积很少用在深度学习中
    • 我们说的反卷积神经网络指用了转置卷积的神经网络

• 总结

  • 转置卷积是一种变化了输入和核的卷积，来得到上采用的目的
  • 不等同于数学上的反卷积操作