序列模型

1.目录

• 序列模型
  • 1.目录
  • 2.序列数据
    • 2.1 更多例子
  • 3.统计工具
  • 4.序列模型
    • 4.1 方案 A:马尔科夫假设
    • 4.2 方案 B:潜变量模型
  • 5.总结
  • 6.Q&A：

2.序列数据

• 实际中很多数据是有时序的
• 电影的评价随时间变化而变化
  • 拿了奖后评分上升，直到奖项被遗忘
  • 看了很多好电影后，人们的期望变高
  • 季节性：贺岁片，暑期档
  • 导演、演员的负面报道导致评分变低

2.1 更多例子

• 音乐、文本、语言和视频都是连续的

  • 标题“狗咬人”远没有“人咬狗”那么令人惊讶

• 大地震发生后，很有可能会有几次较小的余震

• 人的互动是连续的，从网上吵架可以看出

• 预测明天的股价要比填补昨天遗失的股价更困难

3.统计工具

• 在时间 t 观察到，那么得到 T 个不独立的随机变量

• 使用条件概率展开

  

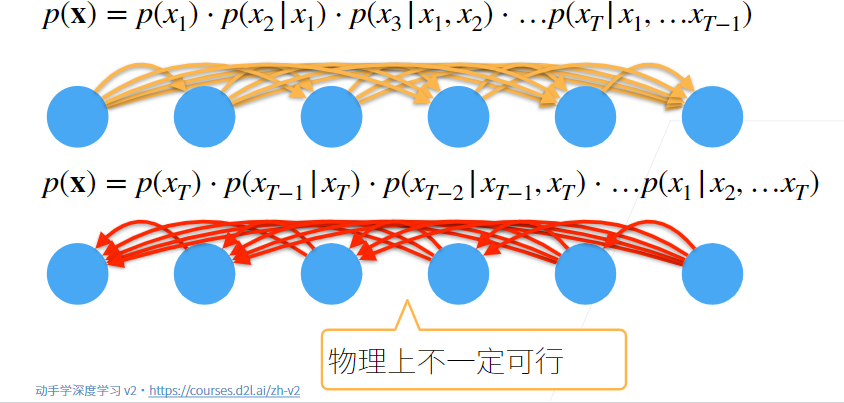
4.序列模型

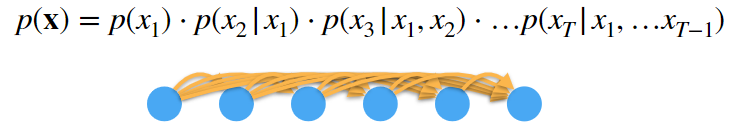
• 对条件概率建模

4.1 方案 A:马尔科夫假设

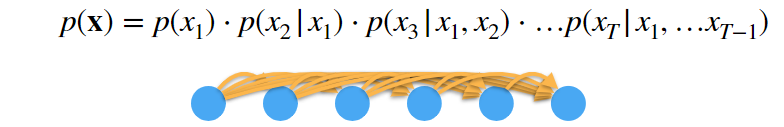
• 假设当前数据只跟 τ 个过去数据点相关

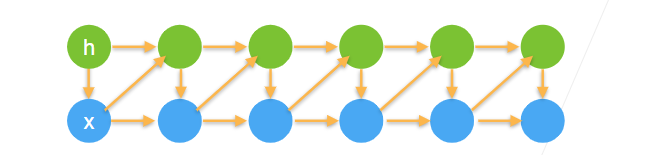
4.2 方案 B:潜变量模型

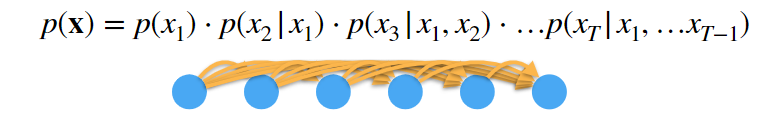
• 引入潜变量来表示过去信息
  • 这样

5.总结

• 时序模型中，当前数据跟之前观察到的数据相关
• 自回归模型使用自身过去数据来预测未来
• 马尔科夫模型假设当前只跟最近少数数据相关，从而简化模型
• 潜变量模型使用潜变量来概括历史信息

6.Q&A：

Q1:在常规范围内 tau 是不是越大越好。刚才例子 tau=5 是不是比 4 好？

当然比 4 好，也有局限性，tau 特别大，训练样本变小，模型变复杂

Q2：潜变量模型和隐马尔科夫模型有什么区别？

没有太多联系，两个不同的观点，但是潜变量模型可以使用隐马尔科夫假设。潜变量-怎么建模，隐马尔科夫-这个数据和之前多少个数据有关。

Q3：若预测一个月，tau=30,预测 7 天，tau=7，是否有这样的关系？

tau 取决于对数据的理解，没有固定的规则

Q4：在预测未来方面，现在的 sota 模型能做到多好？

具体问题具体分析，在有些领域做得好比如写作，写代码，在一些领域做的不好，比如预测股票。

Q5:tau 能够随着 xt 的变化而变化吗？这样感觉更符合实际情况

当然可以，有计算量的增加，也不一定更好

Q6:预测电池之类很多参数的未来变化趋势时怎么长步预测？

与数据关系比较大，负类样本较少，所以比较难训练