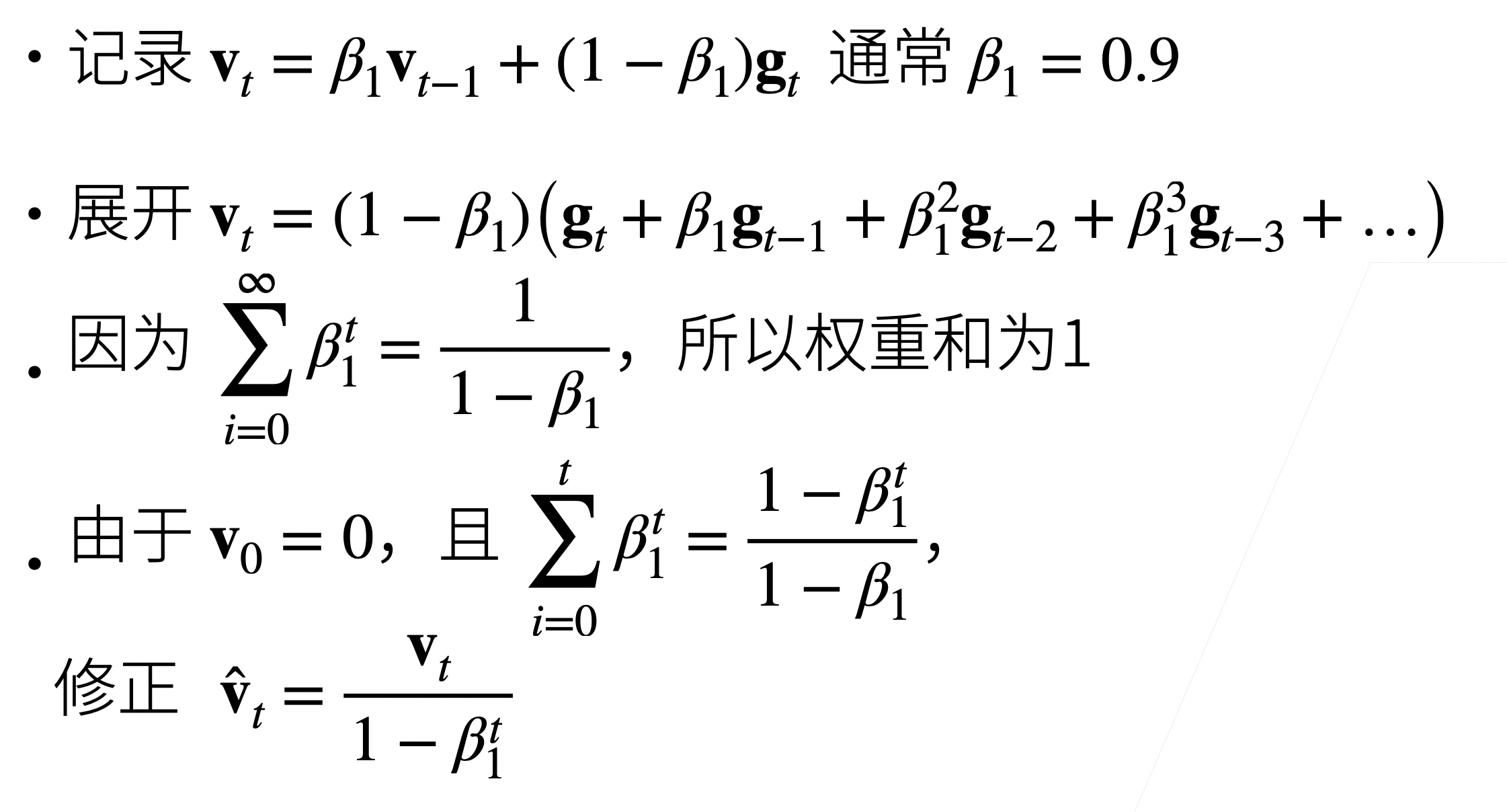72-优化算法
72.优化算法
目录
1.优化问题
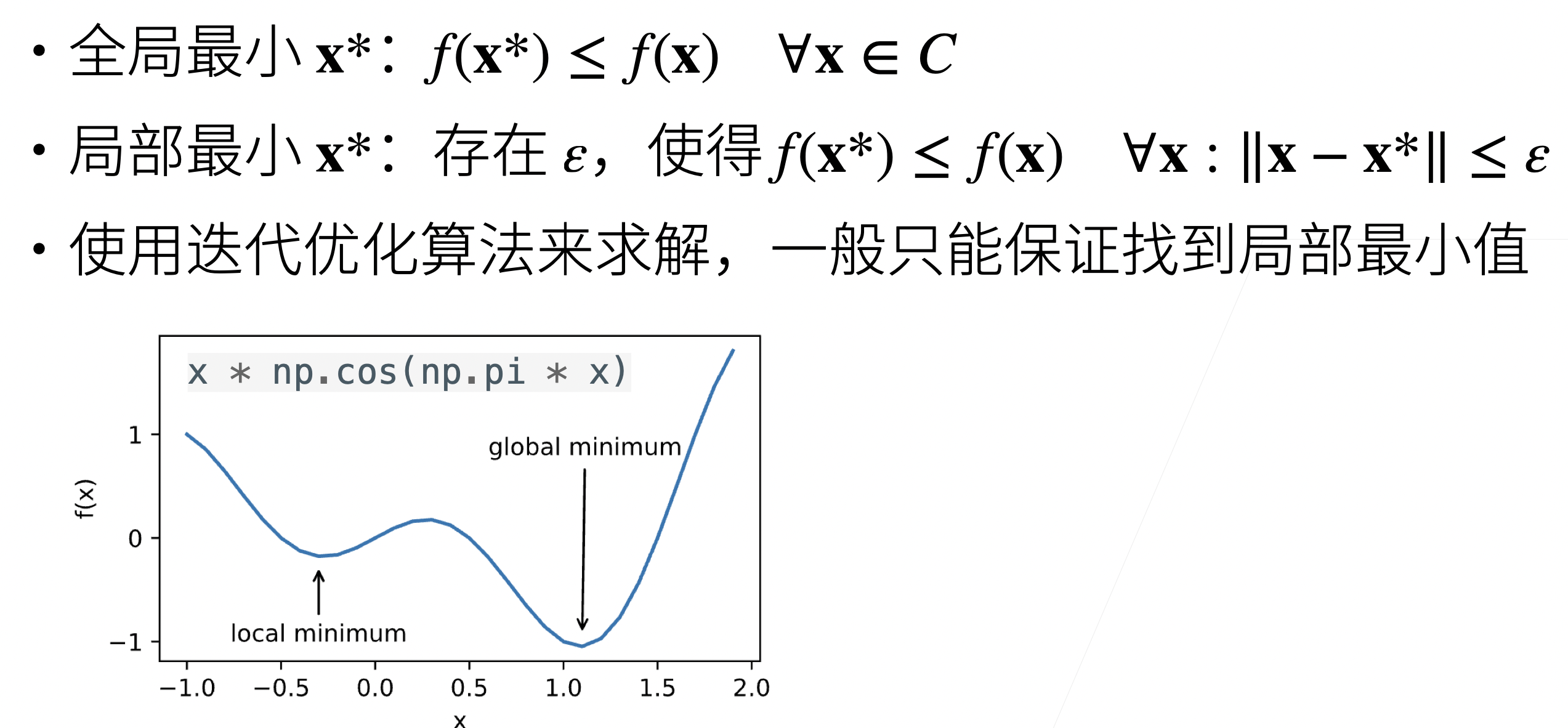
2.局部最小 vs 全局最小
3.凸集和凸函数
- 凸集:形象化来说,就是这个集合上任意两个点连一条线,这个线在集合里面
- 凸函数:形象上来说函数上任取两个点连线,函数都在该线下面
- 凸优化问题:局部最小一定是全局最小。严格凸优化问题有唯一的全局最小。
- 凸:线性回归,softmax 回归
- 非凸:其他(MLP,CNN,RNN,attention)
4.梯度下降
- 梯度下降——最简单的迭代求解算法
- 随机梯度下降
- 求导数需要求所有样本导数,样本多的情况下代价太大
- 理论依据:所用样本,和随机选取一个样本得到的数学期望是一样的。
- 小批量随机梯度下降(实际应用的)
- 计算原因:计算单样本的梯度难以完全利用硬件资源
- 采集一个随机子集
- 理论依据:无偏近,但降低了方差
5.冲量法
- 使用平滑过的梯度对权重更新,不容易震荡
- momentum
6.Adam
- 非常平滑,对于学习率不敏感
- 对于 t 比较小的时候,由于$v_0=0$,所以会导致一开始值比较小,做了一个修正。
- 为什么除以$\sqrt{\widehat{s}_t}+\epsilon$?
- 在 nlp 里面常用,起到正则化的作用,控制每个维度的值在合适的大小。
总结
- 深度学习模型大部分是非凸的
- 小批量随机梯度下降是最常见的优化算法
- 冲量是对梯度做平滑
- Adam 是对梯度做平滑,且对梯度各个维度值做重新调整,对于学习率不敏感