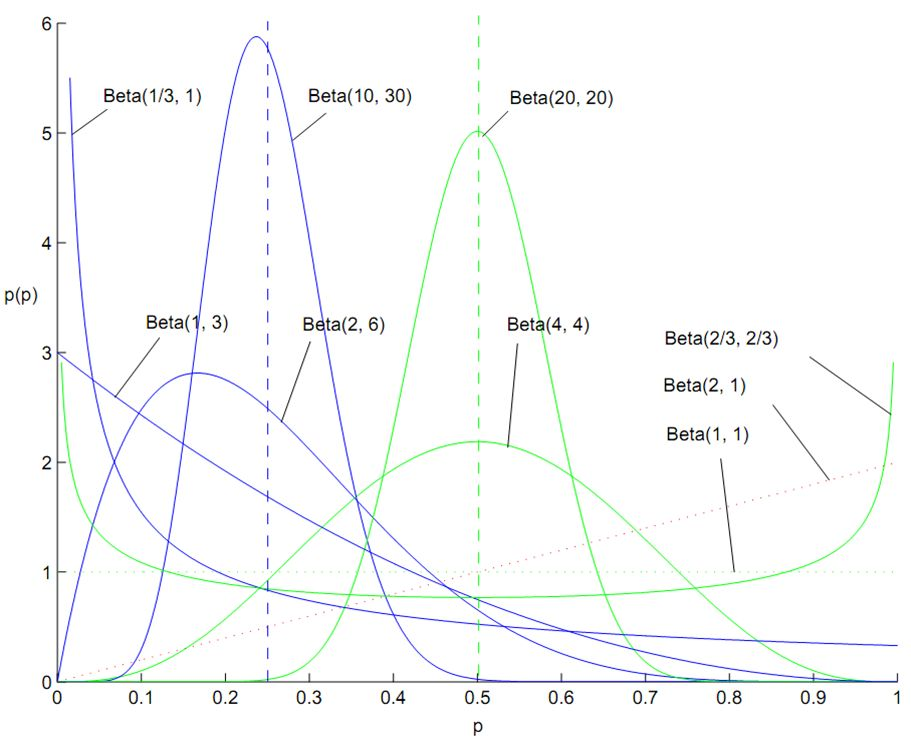
泊松分布
Uniform Distribution | 均匀分布
均匀分布式是定义在区间 $[a,b] (a<b)$ 上连续变量的简单概率分布。对于离散随机变量 $X$,假设其有 $k$ 个取值:$x_{1}, x_{2}, \cdots, x_{k}$,则均匀分布的概率密度函数 PMF 为:
$$ p\left(X=x_{i}\right)=\frac{1}{k}, \quad i=1,2, \cdots, k $$
对于连续随机变量 $X$ 而言,其概率密度函数 PDF 为:
$$ p(X=x)=\left{\begin{array}{ll}{0,} & {x \notin[a, b]} \ {\frac{1}{b-a},} & {x \in[a, b]}\end{array}\right. $$
推导其期望与方差为:
$$ E(X)=\frac{1}{2}(a+b) \ D(X)=\frac{(b-a)^2}{12} $$
不难发现,如果变量 $x$ 服从均匀分布 $U(x|0,1)$ 且 $a<b$,则 $a+(b-a)x$ 服从均匀分布 $U(x|a,b)$.
泊松分布
假设已知事件在单位时间(或者单位面积)内发生的平均次数为 $\lambda$,则泊松分布描述了:事件在单位时间(或者单位面积)内发生的具体次数为 $k$ 的概率。
泊松分布的概率质量函数为:
$$ p(X=k ; \lambda)=\frac{e^{-\lambda} \lambda^{k}}{k !} $$
其期望 $\mathbb{E}[X]=\lambda$,方差 $\operatorname{Var}[X]=\lambda$。
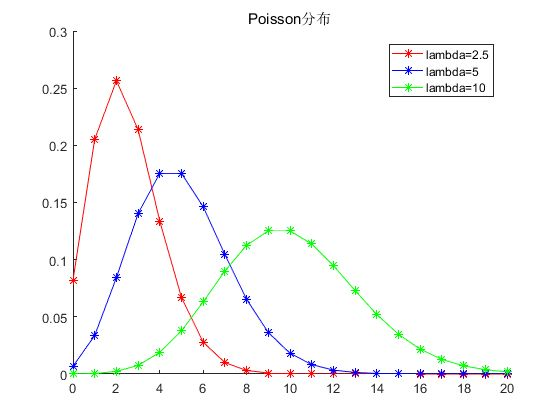
我们可以用均匀分布来模拟泊松分布:
def make_poisson(lmd,tm):
'''
用均匀分布模拟泊松分布。lmd为 lambda 参数;tm 为时间
'''
t=np.random.uniform(0,tm,size=lmd*tm) # 获取 lmd*tm 个事件发生的时刻
count,tm_edges=np.histogram(t,bins=tm,range=(0,tm))#获取每个单位时间内,事件发生的次数
max_k= lmd *2 # 要统计的最大次数
dist,count_edges=np.histogram(count,bins=max_k,range=(0,max_k),density=True)
x=count_edges[:-1]
return x,dist,stats.poisson.pmf(x,lmd)
首先随机性给出了 lmd*tm 个事件发生的时间(时间位于区间 [0,tm])内,
然后统计每个单位时间区间内,事件发生的次数。然后统计这些次数出现的频率,最后将这个频率与理论上的泊松分布的概率质量函数比较。
指数分布
若事件服从泊松分布,则该事件前后两次发生的时间间隔服从指数分布。由于时间间隔是个浮点数,因此指数分布是连续分布。指数分布的概率密度函数为:
$$ p(t ; \lambda)=\left{\begin{array}{ll}{0,} & {t<0} \ {\frac{\lambda}{\exp (\lambda t)},} & {t \geq 0}\end{array}\right. $$
其中 $t$ 为时间间隔,期望为 $\mathbb{E}[t]=\frac{1}{\lambda}$,方差为 $\operatorname{Var}[t]=\frac{1}{\lambda^{2}}$。
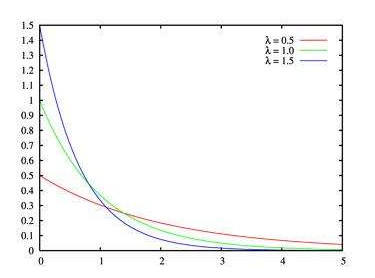
我们同样可以用均匀分布来模拟指数分布:
def make_expon(lmd,tm):
'''
用均匀分布模拟指数分布。lmd为 lambda 参数;tm 为时间
'''
t=np.random.uniform(0,tm,size=lmd*tm) # 获取 lmd*tm 个事件发生的时刻
sorted_t=np.sort(t) #时刻升序排列
delt_t=sorted_t[1:]-sorted_t[:-1] #间隔序列
dist,edges=np.histogram(delt_t,bins="auto",density=True)
x=edges[:-1]
return x,dist,stats.expon.pdf(x,loc=0,scale=1/lmd) #scale 为 1/lambda
伽玛分布
若事件服从泊松分布,则事件第 $i$ 次发生和第 $i + k$ 次发生的时间间隔为伽玛分布。由于时间间隔是个浮点数,因此伽玛分布是连续分布。伽玛分布的概率密度函数为:
$$ p(t ; \lambda, k)=\frac{t^{(k-1)} \lambda^{k} e^{(-\lambda t)}}{\Gamma(k)} $$
其中 $t$ 为时间间隔,伽玛分布的期望为 $\mathbb{E}[t]=\frac{k}{\lambda}$,方差为 $\operatorname{Var}[t]=\frac{k}{\lambda^{2}}$。
上面的定义中 $k$ 必须是整数,若随机变量 $X$ 服从伽玛分布,则其概率密度函数为:
$$ p(X ; \alpha, \beta)=\frac{\beta^{\alpha}}{\Gamma(\alpha)} X^{\alpha-1} e^{-\beta X}, \quad X>0 $$
该分布记作 $\Gamma(\alpha, \beta)$,其中 $\alpha$ 称作形状参数,$\beta$ 称作尺度参数。其期望为 $\mathbb{E}[X]=\frac{\alpha}{\beta}$,方差 $\operatorname{Var}[X]=\frac{\alpha}{\beta^{2}}$。当 $\alpha \leq 1$ 时,$p(X ; \alpha, \beta)$ 为递减函数;当 $\alpha>1$ 时,$p(X ; \alpha, \beta)$ 为单峰函数。
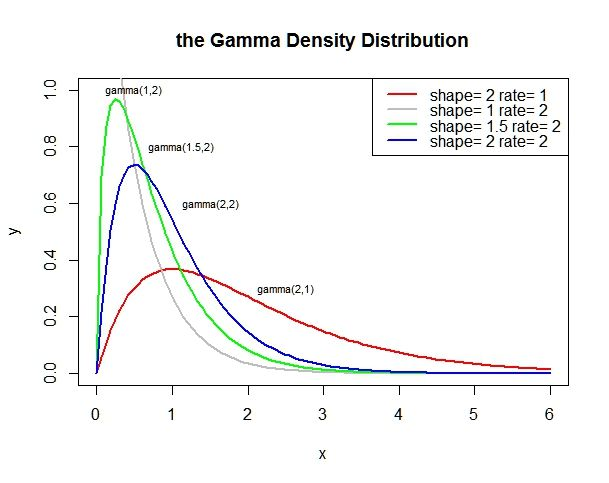
当 $\beta=n$ 时,伽玛分布就是 $Erlang$ 分布。当 $\alpha=1, \beta=\lambda$ 时,就是参数为 $\lambda$ 的指数分布。当 $\alpha=\frac{n}{2}, \beta=\frac{1}{2}$ 时,就是常用的卡方分布。
伽玛分布满足可加性原理,假设随机变量 $X_{1}, X_{2}, \cdots, X_{n}$ 相互独立并且都服从伽玛分布;$X_{i} \sim \Gamma\left(\alpha_{i}, \beta\right)$,则:
$$ X_{1}+X_{2}+\cdots+X_{n} \sim \Gamma\left(\alpha_{1}+\alpha_{2}+\cdots+\alpha_{n}, \beta\right) $$
我们同样可以用均匀分布来模拟伽玛分布:
def make_gamma(lmd,tm,k):
'''
用均匀分布模拟伽玛分布。lmd为 lambda 参数;tm 为时间;k 为 k 参数
'''
t=np.random.uniform(0,tm,size=lmd*tm) # 获取 lmd*tm 个事件发生的时刻
sorted_t=np.sort(t) #时刻升序排列
delt_t=sorted_t[k:]-sorted_t[:-k] #间隔序列
dist,edges=np.histogram(delt_t,bins="auto",density=True)
x=edges[:-1]
return x,dist,stats.gamma.pdf(x,loc=0,scale=1/lmd,a=k) #scale 为 1/lambda,a 为 k
贝塔分布
贝塔分布是定义在 $(0,1)$ 之间的连续概率分布。如果随机变量 $X$ 服从贝塔分布,则其概率密度函数为:
$$ p(X, \alpha, \beta)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} X^{\alpha-1}(1-X)^{\beta-1}=\frac{1}{B(\alpha, \beta)} X^{\alpha-1}(1-X)^{\beta-1}, \quad 0 \leq X<1 $$
上述分布记作 $\operatorname{Beta}(\alpha, \beta)$,贝塔分布的期望为 $\mathbb{E}[X]=\frac{\alpha}{\alpha+\beta}$,方差为 $\operatorname{Var}[X]=\frac{\alpha \beta}{(\alpha+\beta)^{2}(\alpha+\beta+1)}$。