线性代数基础

1、向量是什么

1.1、向量的定义

在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小和方向的量。它可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。与向量对应的量叫做数量（物理学中称标量），数量（或标量）只有大小，没有方向。

1.2、向量的表示

向量的记法：印刷体记作粗体的字母（如a,b,u,v），书写时在字母顶上加一小箭头’‘→’’。如果给定向量的起点（A）和终点（B），可将向量记作 $\vec{AB}$​​ 。实际上向量有多种记法，可以用元组表示一个向量，如 $(x_1,x_2)$​ 或 $<x_1,x_2>$​​。在线性代数中，n 元向量可以用 n×1 矩阵表示，如：

$V = \left[\begin{aligned}&x_1\&x_2\&x_3\&x_4\&…\&x_n\end{aligned}\right]$

或者

$V^T = [x_1,x_2,x_3,x_4,…,x_n]$

向量中的每个元素 $x_n$​ ，都称作向量的一个分量。

1.3、向量物理意义

$\vec{OM} = (P,Q,R)$​

$\vec{OM} = \vec{OP} + \vec{OQ} + \vec{OR}$

向量的几何意义就是空间中的点，物理意义就是速度或者力这样的矢量。

向量的分量我们称之为维度，n 维向量集合的全体就构成了 n 维欧式空间，一个 n 维向量其实就是一个 n 维欧式空间的一个点。

2、行向量与列向量

行向量在线性代数中，是一个 $1 \times n$​​ 的矩阵，即矩阵由一个含有 n 个元素的行所组成即行向量。行向量的转置是一个列向量，反之亦然。

行向量示例：

$V = [x_1,x_2,…,x_n]$

在线性代数中，列向量是一个 n×1 的矩阵，即矩阵由一个含有 n 个元素的列所组成。

列向量示例：

$V = \left[\begin{aligned}&x_1\&x_2\&…\&x_n\end{aligned}\right]$​

为简化书写、方便排版起见，有时会以加上转置符号 T 的行向量表示列向量。

$V = [x_1,x_2,…,x_n]^T$

在机器学习中说道向量一般都是指列向量。

3、向量运算

3.1、向量加减法

等于它们的分量分别相加，显然两个向量的长度得是相等的，减法我们在这里不列举，很容易举一反三。

$\left[\begin{aligned}2\4\2\end{aligned}\right] + \left[\begin{aligned}3\1\7\end{aligned}\right] = \left[\begin{aligned}5\5\9\end{aligned}\right]$

3.2、向量数乘

$3 \times \left[\begin{aligned}3\1\2\end{aligned}\right] = \left[\begin{aligned}9\3\6\end{aligned}\right]$​​​

3.3、转置

$\left[\begin{aligned}2\4\2\end{aligned}\right]^T = [2,4,2]$

$[7,0,-3]^T = \left[\begin{aligned}7\0\-3\end{aligned}\right] $​​

3.4、向量内积

两个列向量， $A^TB$​，等于对应位置相乘再相加。

$[2,7,3] \cdot \left[\begin{aligned}3\1\7\end{aligned}\right] = 2\times 3 + 7\times 1 + 3 \times 7 = 34$​​

3.5、向量运算法则

1、实数与向量运算法则，设$\lambda ，\mu$ 是实数，则有：

• 结合律：$\lambda(\mu A) = (\lambda\mu)A$

• 分配律：$(\lambda + \mu)A = \lambda A + \mu A$ ， $\lambda(A + B) = \lambda A + \lambda B$

2、向量内积运算法则

• 交换律：$A\cdot B = B\cdot A$

• 分配律：$(A + B)\cdot C = A\cdot C + B\cdot C$​

• 结合律：$(\lambda A)\cdot B = \lambda(A\cdot B)$

4、向量的范数

范数的公式是向量每个分量绝对值 P 次方 再用幂函数计算 P 分之一，这里 P 肯定是整数 1，2，3…到正无穷都是

可以的。向量的范数就是把向量变成一个标量，范数的表示就是两个竖线来表示，然后右下角写上 P。

$||A||P = \left [ \sum\limits{i = 1}^n|a_i|^P\right ]^{\frac{1}{P}}$

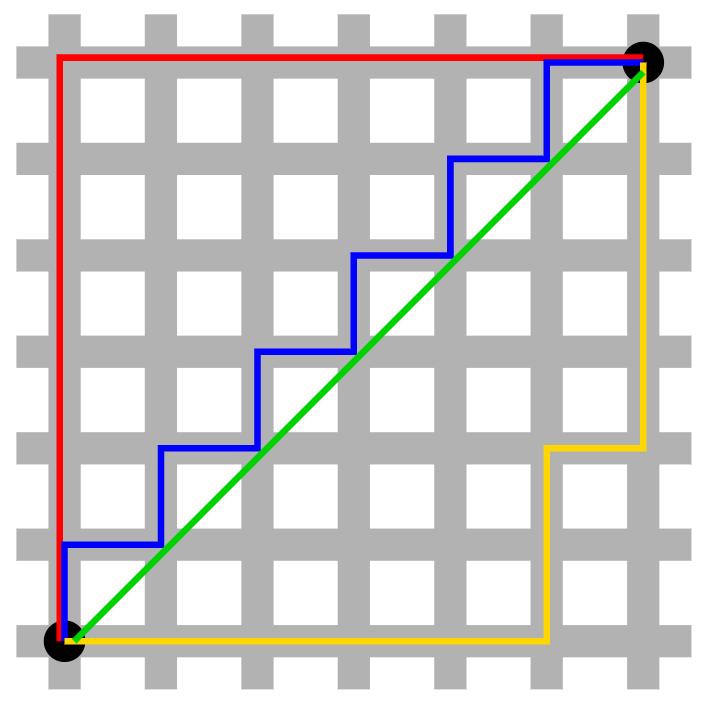
1-范数

$||X||1 = \sum\limits{i = 1}^n|x_i|$​​

即向量元素绝对值之和，表示 X 到零点的曼哈顿距离，如上图：红色、蓝色、黄色的线条。

2-范数

$||X||2 = \sqrt{\sum\limits{i=1}^nx_i^2}$​​

即向量元素的平方和再开方，也叫欧几里得范数，常用计算向量长度，表示 X 到零点的欧式距离。

P-范数

$||X||P = \left [ \sum\limits{i = 1}^n|x_i|^P\right ]^{\frac{1}{P}}$​

即向量元素绝对值的 P 次方和的 $\frac{1}{P}$​ 次幂，表示 X 到零点的 P 阶闵氏距离。

$\infty $​-范数

$||X||{\infty} = \max\limits{i}|x_i|$​​​

当 P 趋向于正无穷时，即所有向量元素绝对值中的最大值。表示切比雪夫距离。

国际象棋棋盘上二个位置间的切比雪夫距离是指王要从一个位子移至另一个位子需要走的步数。由于王可以往斜前或斜后方向移动一格，因此可以较有效率的到达目的的格子。

$-\infty $-范数

$||X||{-\infty} = \min\limits{i}|x_i|$​

当 P 趋向于负无穷时，即所有向量元素绝对值中的最小值。

5、特殊向量

0 向量

就是分量全部为 0 的向量

$[0,0,…,0]$

单位向量

就是 2-范数为 1、模为 1、长度为 1 的向量。

向量$\vec{AB}$​ 的长度叫做向量的模，记作 $|\vec{AB}|$。

计算公式：

• 空间向量(x,y,z)，其中 x,y,z 表示三个轴上的坐标，模长为：$\sqrt{x^2 + y^2 + z^2}$。
• 平面向量(x,y)， 模长为：$\sqrt{x^2 + y^2}$

根据 2-范数的公式可知，2-范数就是向量的模，对于向量（列向量）来说，2-范数就是：

$X^TX$

6、矩阵是什么

矩阵就是二维数组，下面是一个 m 乘 n 的矩阵，它有 m 行，n 列，每行每列上面都有元素，每个元素都有行标

i 和列标 j， $a_{ij}$ 。简称 m × n 矩阵，记作：

$ A = \left{ \begin{matrix}a_{11}  & \cdots & a_{1n} \ a_{21}  & \cdots & a_{2n} \ \vdots & \ddots & \vdots \ a_{m1}  & \cdots & a_{mn}\end{matrix} \right} $​​​​​​​​​

注意$a_{11}$​​ 的索引是 A[0,0]。

这 m×n 个数称为矩阵 A 的元素，简称为元，数$a_{ij}$位于矩阵 A 的第 i 行第 j 列，称为矩阵 A 的 $(i,j)$ 元，m×n 矩

阵 A 也记作 $A_{mn}$ 。

7、常见矩阵

7.1、方阵

如果 m 等于 n，那就称为方阵

$ A = \left [ \begin{matrix}1 & 11 & 3 \ 4 & 9 & 2 \ 7 & 5 & 1\end{matrix} \right ] $​​​​

7.2、对称矩阵

定义是 $a_{ij}$ 等于 $a_{ji}$ 那么就是对称矩阵，对称矩阵首先是个方阵

$ A = \left [ \begin{matrix}1 & 4 & 7 \ 4 & 9 & 2 \ 7 & 2 & 1\end{matrix} \right ] $​

7.3、单位矩阵

主对角线都是 1，其它位置是 0，这称之为单位矩阵，单位矩阵写为 $I$，一定是方阵，等同于数字里面的 1。

$ A = \left [ \begin{matrix}1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1\end{matrix} \right ] $​

7.4、对角矩阵

对角矩阵，就是主对角线非 0，其它位置是 0。

$A = \left[\begin{matrix}\lambda_1 &\cdots &0&0&0\0&\lambda_2&0&0&0\0&\cdots&\cdots&\cdots&0\0&0&\cdots&\cdots&\cdots\0&0&0&\cdots&\lambda_n\end{matrix}\right]$​​​

对角矩阵一定是方阵。不然没有对角线！

8、矩阵运算

8.1、矩阵加减法

矩阵的加法就是矩阵的对应位置相加，减法也是一样就是对应位置相减。

$\left[\begin{matrix}1&3\2&7\5&4\end{matrix}\right] + \left[\begin{matrix}4&6\0&3\2&1\end{matrix}\right] = \left[\begin{matrix}5&9\2&10\7&5\end{matrix}\right]$

8.2、数乘

$3 \times \left[\begin{matrix}1&3&5\2&4&3\end{matrix}\right] = \left[\begin{matrix}3&9&15\6&12&9\end{matrix}\right]$​​

8.3、矩阵乘法

矩阵的乘法和一般的乘法是不太一样！

它是把第一个矩阵的每一行，和第二个矩阵的每一列拿过来做内积得到结果。

$\left[\begin{matrix}1&2&1\3&1&0\end{matrix}\right] \cdot\left[\begin{matrix}2&5\0&4\7&2\end{matrix}\right] = \left[\begin{matrix}9&15\6&19\end{matrix}\right] $​​

矩阵乘法运算结果

$\rm m \times n \ \cdot \ n\times k = m \times k$​

8.4、矩阵转置

转置的操作和向量是一样的，就是把 $a_{ij}$ 变成 $a_{ji}$​，把行和列互换一下

$\left[\begin{matrix}1&2&1\3&1&0\end{matrix}\right]^T = \left[\begin{matrix}1&3\2&1\1&0\end{matrix}\right]$

8.4、矩阵运算法则

矩阵加减法

满足：分配律、结合律、交换律

$A + B + C = (A + C) + B$

矩阵乘法

• 满足结合律

$(AB)C = A(BC)$​

• 满足分配律

$(A + B)C = AC + BC$​ ，左分配律

$A(B + C) = AB + AC$​ ，右分配律

• 不满足交换律

不一定相等，甚至 AB 的尺寸和 BA 的尺寸是不同的。

$AB \not= BA$​

$\left[\begin{matrix}1&2&1\3&1&0\end{matrix}\right] \cdot\left[\begin{matrix}2&5\0&4\7&2\end{matrix}\right] = \left[\begin{matrix}9&15\6&19\end{matrix}\right] $

$\left[\begin{matrix}2&5\0&4\7&2\end{matrix}\right] \cdot \left[\begin{matrix}1&2&1\3&1&0\end{matrix}\right] = \left[\begin{matrix}17&9&2\12&4&0\13&16&7\end{matrix}\right] $​​​​​​​​​​

矩阵乘法 + 转置

$(AB)^T = B^TA^T$

9、逆矩阵

9.1、逆矩阵定义

矩阵有 AB 云散，但是没有 A/B 这么一说，只有逆矩阵。

逆矩阵怎么定义的？

假设有个矩阵 A，注意它一定是方阵（必须是方阵），乘以矩阵 B 等于单位矩阵 $I$​ ：

$AB = I$ 或者 $BA = I$​

那么我们称这里的 B 为 A 的右逆矩阵，和左逆矩阵。

有个很重要的结论就是，如果这样的 B 存在的话，它的左逆和右逆一定相等，统称为 A 的逆矩阵 $A^{-1}$。则：

$A = B^{-1}$

$B = A^{-1}$

9.2、逆矩阵作用

矩阵求逆有什么用呢？它可以帮助我们解线性方程组，比如 $XW = Y$​ 。两边同时乘以 X 的逆：

$X^{-1}XW = X^{-1}Y$

$(X^{-1}X)W = X^{-1}Y$

$IW = X^{-1}Y$​

$W = X^{-1}Y$

就可以求解出方程的系数，它发明的目的也是干这样的事情用的。

举例说明：

# 三元一次方程
# 3x + 2y + 4z = 19
# 2x -y + 3z = 9
# x + y - z = 0
import numpy as np
X = np.array([[3,2,4],[2,-1,3],[1,1,-1]])
Y = np.array([19,9,0])

display(X,Y)

# np.linalg.inv表示矩阵求逆
# dot表示矩阵乘法
W = np.linalg.inv(X).dot(Y)
print('求解方程得x,y,z为：',W)
'''
array([[ 3,  2,  4],
       [ 2, -1,  3],
       [ 1,  1, -1]])
array([19,  9,  0])
求解方程得x,y,z为： [1. 2. 3.]
'''

从这里我们也可以看出来单位矩阵像我们乘法里面的 1。

逆矩阵相关公式：

• $(AB)^{-1} = B^{-1}A^{-1}$
• $(A^{-1})^{-1} = A$
• $(A^T)^{-1} = (A^{-1})^T$​

10、行列式

行列式其实在机器学习中用的并不多，一个矩阵必须是方阵，才能计算它的行列式

行列式是把矩阵变成一个标量

$\left |\begin{matrix}a_{11}&a_{12}\a_{21}&a_{22}\end{matrix}\right| = a_{11}a_{22} - a_{12}a_{21}$​

import numpy as np
A = np.array([[1,3],[2,5]])
display(A)
print('矩阵A的行列式是：\n',np.linalg.det(A))
'''
array([[1, 3],
       [2, 5]])
矩阵A的行列式是：
 -1.0
'''

行列式在求解，逆矩阵的过程中，起到了作用，行列式不为 0，才可以求解逆矩阵！

import numpy as np
A = np.array([[1,3],[2,6]])
display(A)
print('矩阵A的行列式是：\n',np.linalg.det(A))
'''
array([[1, 3],
       [2, 6]])
矩阵A的行列式是：
 0.0
'''
# 无法求解行列式，报错信息：LinAlgError: Singular matrix
print('矩阵A的逆矩阵为：\n',np.linalg.inv(A))

11、伴随矩阵

11.1、伴随矩阵定义

设有一矩阵 $A$

设 $A_{ij}$ 是矩阵 A 中元素 $a_{ij}$​ 的代数余子式，那么矩阵 $A^*$

称为矩阵 $A$​ 的伴随矩阵

11.2、代数余子式

1、代数余子式定义

2、代数余子式计算

计算过程如下：

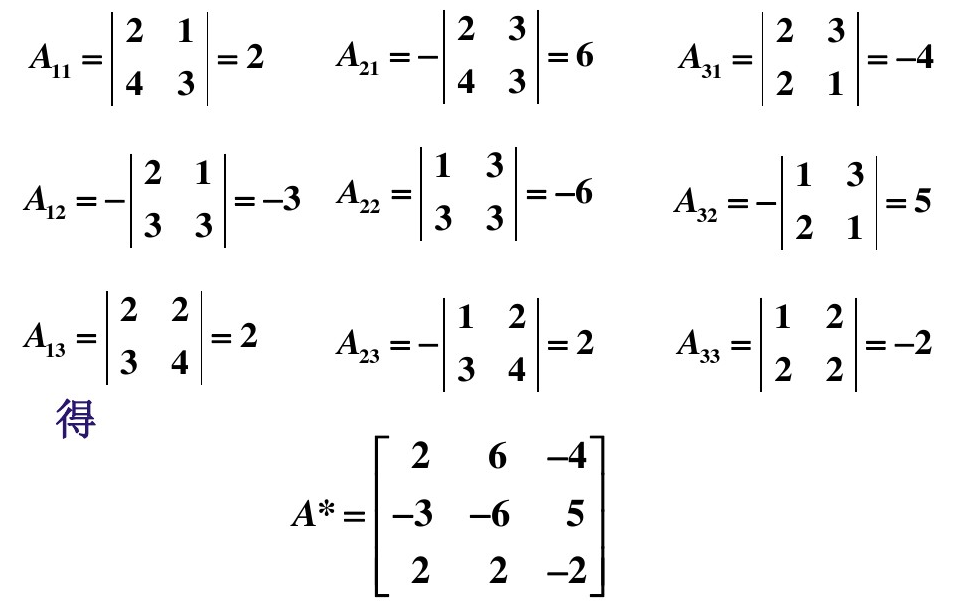
11.3、伴随矩阵性质

$AA^* = A^*A = |A|E$​

$AA^* = A^*A = |A|I$

$I,E$ 都表示单位矩阵。

11.4、伴随矩阵与逆矩阵

$AA^{-1} = I$​

$AA^* = |A|I$​ ，其中|A| 是行列式

$A\frac{A^*}{|A|} = I$​​

根据上式可得：

$A^{-1} = \frac{A^*}{|A|}$

import numpy as np
# 声明矩阵
A = np.array([
    [1,2,3],
    [2,2,1],
    [3,4,3]])
A_bs = [] # 伴随矩阵
n = 3 # A方阵的行、列数量
for i in range(n):
    for j in range(n):
        row = [0,1,2] # 行索引
        col = [0,1,2] # 列索引
        row.remove(i) # 去除行
        col.remove(j) # 去除列
        # 代数余子式
        A_ij = A[np.ix_(row,col)]
        A_bs.append(((-1)**(i+j)) * np.linalg.det(A_ij))
A_bs = np.array(A_bs).reshape(3,3).T
print('根据伴随矩阵求逆矩阵：\n',A_bs/np.linalg.det(A))
print('用NumPy模块求逆矩阵 ：\n',np.linalg.inv(A))
'''
根据伴随矩阵求逆矩阵：
 [[ 1.   3.  -2. ]
 [-1.5 -3.   2.5]
 [ 1.   1.  -1. ]]
用NumPy模块求逆矩阵 ：
 [[ 1.   3.  -2. ]
 [-1.5 -3.   2.5]
 [ 1.   1.  -1. ]]
'''