调度算法
柔性作业车间调度问题的研究方法
从 Johnson 揭开调度问题研究的序幕以来,调度问题一直是极其困难的组合优化问题,调度模型从简单到复杂,研究方法也随着调度模型的变迁从开始的数学方法到启发式的智能算法。目前解决调度问题的方法主要分为两类:精确方法(exact method)和近似方法(approximation method)。精确方法也可称为最优化方法,能够保证得到全局最优解,但只能解决较小规模的问题,而且速度很慢。近似方法求解时,可以很快地得到问题的解,但不能保证得到的解是最优的,不过对于大规模问题是非常合适的,可以较好地满足实际问题的需求。下图为近年来求解调度问题的主要研究方法。
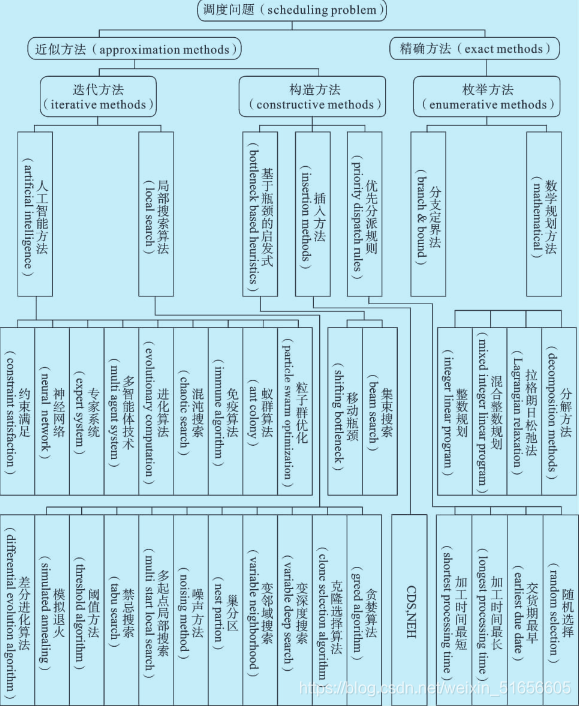
精确方法
精确方法主要包括整数规划、混合整数规划、拉格朗日松弛法、分解方法及分支定界法等。
数学规划方法
数学规划方法中求解调度问题的最常见方法是混合整数规划。混合整数规划有一组线性约束和一个线性目标函数,该方法限制决策变量都必须是整数。导致在运算中出现的整数个数以指数规模增长,即便使用更好更简洁的公式表述,也需要大量的约束条件。较多成功的数学模型的建立都归功于拉格朗日松弛法(Lagrangian relaxation)和分解方法(decomposition method)。拉格朗日松弛法用非负拉格朗日乘子将工艺约束和资源约束进行松弛,最后将惩罚函数加入目标函数中。上海交通大学的刘学英用拉格朗日松弛法解决车间调度问题。分解方法将原问题分解为多个小的易于解决的子问题,然后对子问题寻找最优。
