共识算法

分布式共识

共识（Consensus）是分布式计算中最重要也是最基本的问题之一，所谓共识，就是让所有的节点对某件事达成一致；例如，如果有几个人同时尝试预订飞机上的最后一个座位，或剧院中的同一个座位，或者尝试使用相同的用户名注册一个帐户，共识算法可以用来确定这些互不相容的操作中，哪一个才是赢家。

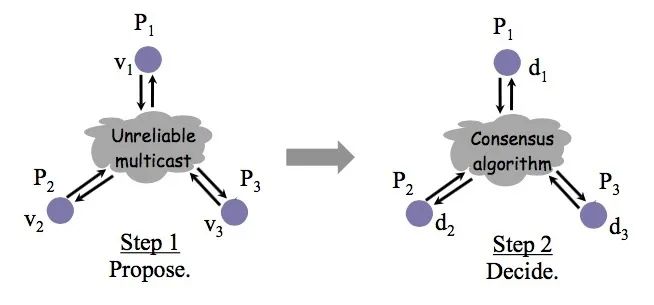
因为分布式系统中存在着的网络故障与流程故障，可靠地达成共识是一个令人惊讶的棘手问题。一旦达成共识，应用可以将其用于各种目的。共识的典型场景包括了：

领导选举：在单主复制的数据库中，所有节点需要就哪个节点是领导者达成一致。如果一些节点由于网络故障而无法与其他节点通信，则可能会对领导权的归属引起争议。在这种情况下，共识对于避免错误的故障切换非常重要。错误的故障切换会导致两个节点都认为自己是领导者。如果有两个领导者，它们都会接受写入，它们的数据会发生分歧，从而导致不一致和数据丢失。
原子提交：在支持跨多节点或跨多分区事务的数据库中，一个事务可能在某些节点上失败，但在其他节点上成功。如果我们想要维护事务的原子性，我们必须让所有节点对事务的结果达成一致：要么全部中止/回滚（如果出现任何错误），要么它们全部提交（如果没有出错）。这个共识的例子被称为原子提交（atomic commit）问题。

注意，原子提交的形式化与共识稍有不同：原子事务只有在所有参与者投票提交的情况下才能提交，如果有任何参与者需要中止，则必须中止。共识则允许就任意一个被参与者提出的候选值达成一致。然而，原子提交和共识可以相互简化为对方，非阻塞原子提交则要比共识更为困难。近年来随着分布式系统的规模越来越大，对可用性和共识的要求越来越高，分布式共识的应用也越来越广泛。纵观分布式共识在工业界的应用，从最开始的鼻祖 Paxos 的一统天下，到横空出世的 Raft 的流行，再到如今 Leaderless 的 EPaxos 开始备受关注。共识算法根据容错能力不同，即在考虑节点故障不响应的情况下，再考虑节点是否会伪造信息进行恶意响应，可以分为 CFT（Crash Fault Tolerance）类和 BFT（Byzantine Fault Tolerance）类共识算法。

CFT 共识算法只保证分布式系统中节点发生宕机错误时整个分布式系统的可靠性，而当系统中节点违反共识协议的时候（比如被黑客攻占，数据被恶意篡改等）将无法保障分布式系统的可靠性，因此 CFT 共识算法目前主要应用在企业内部的封闭式分布式系统中，目前流行的 CFT 共识算法主要有 Paxos 算法及其衍生的 Raft 共识算法。
采用 BFT 共识算法的分布式系统，即使系统中的节点发生了任意类型的错误，只要发生错误的节点少于一定比例，整个系统的可靠性就可以保证。因此，在开放式分布式系统中，比如区块链网络，必须采用 BFT 共识算法。

共识的局限性

共识算法对于分布式系统来说是一个巨大的突破：它为其他充满不确定性的系统带来了基础的安全属性（一致同意，完整性和有效性），然而它们还能保持容错（只要多数节点正常工作且可达，就能取得进展）。它们提供了全序广播，因此它们也可以以一种容错的方式实现线性一致的原子操作。尽管如此，它们并不是在所有地方都用上了，因为好处总是有代价的。节点在做出决定之前对提议进行投票的过程是一种同步复制，但是通常数据库会配置为异步复制模式。在这种配置中发生故障切换时，一些已经提交的数据可能会丢失；但是为了获得更好的性能，许多人选择接受这种风险。

共识系统总是需要严格多数来运转。这意味着你至少需要三个节点才能容忍单节点故障（其余两个构成多数），或者至少有五个节点来容忍两个节点发生故障（其余三个构成多数）。如果网络故障切断了某些节点同其他节点的连接，则只有多数节点所在的网络可以继续工作，其余部分将被阻塞。大多数共识算法假定参与投票的节点是固定的集合，这意味着你不能简单的在集群中添加或删除节点。共识算法的**动态成员扩展（dynamic membership extension）**允许集群中的节点集随时间推移而变化，但是它们比静态成员算法要难理解得多。

共识系统通常依靠超时来检测失效的节点。在网络延迟高度变化的环境中，特别是在地理上散布的系统中，经常发生一个节点由于暂时的网络问题，错误地认为领导者已经失效。虽然这种错误不会损害安全属性，但频繁的领导者选举会导致糟糕的性能表现，因系统最后可能花在权力倾扎上的时间要比花在建设性工作的多得多。有时共识算法对网络问题特别敏感。例如 Raft 已被证明存在让人不悦的极端情况：如果整个网络工作正常，但只有一条特定的网络连接一直不可靠，Raft 可能会进入领导频繁二人转的局面，或者当前领导者不断被迫辞职以致系统实质上毫无进展。其他一致性算法也存在类似的问题，而设计能健壮应对不可靠网络的算法仍然是一个开放的研究问题。

共识算法

分布式共识

共识的局限性

Links